Интеграл степенной функции
Интеграл от ![]() равен основанию в степени на единицу больше, деленному на эту степень плюс константа интегрирования
равен основанию в степени на единицу больше, деленному на эту степень плюс константа интегрирования
![Rendered by QuickLaTeX.com \[ \int{{{x}^{n}}dx}=\frac{{{x}^{n+1}}}{n+1}+C \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-d108bcc0557ca20e8a9dcc6cbf965ab5_l3.png)
Примеры решения задач
ПРИМЕР 1
| Задание | Найти интеграл |
| Решение | Согласно формуле имеем:
|
| Ответ | 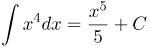 |
ПРИМЕР 2
| Задание | Найти неопределенный интеграл
|
| Решение | Запишем подынтегральную функцию в виде степенной функции по формулам:
и Будем иметь: |
| Ответ | 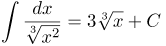 |






![Rendered by QuickLaTeX.com \[\int{\frac{dx}{\sqrt[3]{{{x}^{2}}}}}=\int{\frac{dx}{{{x}^{\frac{2}{3}}}}}=\int{{{x}^{^{-\frac{2}{3}}}}dx}=\frac{{{x}^{^{-\frac{2}{3}+1}}}}{-\frac{2}{3}+1}+C=\frac{{{x}^{^{\frac{1}{3}}}}}{\frac{1}{3}}+C=3\sqrt[3]{x}+C\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-7f191b2292b3058f40ed5f49664f165d_l3.png)





