Первообразная и неопределенный интеграл
![]()
![]()
Константа интегрирования
Доказательство. Так как ![]() – первообразная функции
– первообразная функции ![]() , то по определению имеем, что
, то по определению имеем, что
![]()
Рассмотрим функцию ![]() и покажем, что она также является первообразной для функции
и покажем, что она также является первообразной для функции ![]() . Найдем производную:
. Найдем производную:
![]()
То есть ![]() , а это означает, что и функция
, а это означает, что и функция ![]() является первообразной для функции
является первообразной для функции ![]() .
.
Что и требовалось доказать.
Правила нахождения первообразных
- Если
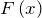 – первообразная для функции
– первообразная для функции 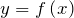 , а
, а 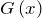 – первообразная функции
– первообразная функции 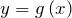 , то
, то 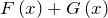 – первообразная функции
– первообразная функции 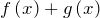 .
. - Если
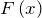 – первообразная для функции
– первообразная для функции 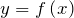 , а
, а 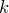 – некоторое число, то
– некоторое число, то 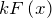 является первообразной для функции
является первообразной для функции 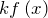 .
. - Если
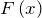 является первообразной функции
является первообразной функции 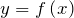 , а
, а 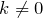 и
и 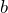 – некоторые числа, то функция
– некоторые числа, то функция 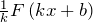 – первообразная для функции
– первообразная для функции 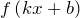 .
.
![]()
Здесь ![]() – знак интеграла,
– знак интеграла, ![]() – подынтегральное выражение,
– подынтегральное выражение, ![]() – подынтегральная функция,
– подынтегральная функция, ![]() – переменная интегрирования.
– переменная интегрирования.











