Несобственный интеграл

ОПРЕДЕЛЕНИЕ

Определенный интеграл от непрерывной функции, но с бесконечным промежутком интегрирования, или определенный интеграл по конечному промежутку, но от функции, терпящей на этом промежутке разрыв, называется несобственным интегралом.

Несобственный интеграл первого рода

ОПРЕДЕЛЕНИЕ

Пусть функция $y=f\left( x \right)$ непрерывна на промежутке $\left[ a;\ +\infty \right)$ . Если существует конечный предел $\underset{b\to \infty }{\mathop{\lim }}\,\int\limits_{a}^{b}{f\left( x \right)dx}$ , то он называется несобственным интегралом первого рода и обозначается $\int\limits_{a}^{\infty }{f\left( x \right)dx}$ .

Таким образом, по определению

$\int\limits_{a}^{+\infty }{f\left( x \right)dx}=\underset{b\to +\infty }{\mathop{\lim }}\,\int\limits_{a}^{b}{f\left( x \right)dx}$

Если такой предел существует, то говорят, что несобственный интеграл $\int\limits_{a}^{\infty }{f\left( x \right)dx}$ сходится. В противном случае, если предел не существует или бесконечен, то несобственный интеграл является расходящимся.

Аналогичным образом задается несобственный интеграл на промежутке $\left( -\infty ;\ b \right]$ .

Несобственный интеграл первого рода с двумя бесконечными пределами определяется формулой:

$\int\limits_{-\infty }^{+\infty }{f\left( x \right)dx}=\int\limits_{-\infty }^{c}{f\left( x \right)dx}+\int\limits_{c}^{+\infty }{f\left( x \right)dx}$

Такой несобственный интеграл сходится только в том случае, когда оба несобственных интеграла в правой части являются сходящимися.

Примеры решения задач

ПРИМЕР 1

Задание	Вычислить несобственный интеграл или установить его расходимость. $\int\limits_{1}^{+\infty }{\frac{dx}{{{x}^{2}}}}$
Решение	Заданный интеграл является несобственным интегралом первого рода, так как на промежутке интегрирования $\left[ 1;\ +\infty \right)$ подынтегральная функция $f\left( x \right)=\frac{1}{{{x}^{2}}}$ является непрерывной, но один из пределов интегрирования равен бесконечности. Тогда, согласно определению, имеем: $\int\limits_{1}^{+\infty }{\frac{dx}{{{x}^{2}}}}=\underset{a\to +\infty }{\mathop{\lim }}\,\int\limits_{1}^{a}{\frac{dx}{{{x}^{2}}}}=-\underset{a\to +\infty }{\mathop{\lim }}\,\left. \frac{1}{x} \right\|_{0}^{a}=-\underset{a\to +\infty }{\mathop{\lim }}\,\left( \frac{1}{a}-1 \right)=-\left( 0-1 \right)=1$
Ответ

ПРИМЕР 2

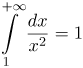Задание

Решить несобственный интеграл или установить его расходимость.

$\int\limits_{1}^{+\infty }{\frac{dx}{x}}$

Решение

Рассматриваемый интеграл является несобственным интегралом первого рода, так как функция $f\left( x \right)=\frac{1}{x}$ на полубесконечном промежутке $\left[ 1;\ +\infty \right)$ непрерывна, но правый предел интегрирования бесконечен. Согласно определению, перейдем к границе

$\int\limits_{1}^{+\infty }{\frac{dx}{x}}=\underset{a\to +\infty }{\mathop{\lim }}\,\int\limits_{1}^{a}{\frac{dx}{x}}=\underset{a\to +\infty }{\mathop{\lim }}\,\left. \ln x \right|_{1}^{a}=\underset{a\to +\infty }{\mathop{\lim }}\,\left( \ln a-0 \right)=+\infty$

то есть интеграл расходится.

Ответ

Интеграл расходится.

Несобственный интеграл второго рода

Пусть некоторая функция $y=f\left( x \right)$ непрерывна на промежутке $\left[ a;\ b \right)$ , а в точке $x=b$ имеет разрыв второго рода. Если существует конечный предел $\underset{\varepsilon \to 0}{\mathop{\lim }}\,\int\limits_{a}^{b-\varepsilon }{f\left( x \right)dx}$ , то он называется несобственным интегралом второго рода и обозначается $\int\limits_{a}^{b}{f\left( x \right)dx}$ , то есть

$\int\limits_{a}^{b}{f\left( x \right)dx}=\underset{\varepsilon \to 0}{\mathop{\lim }}\,\int\limits_{a}^{b-\varepsilon }{f\left( x \right)dx}$

Если предел в правой части существует, то несобственный интеграл второго рода называется сходящимся. В случае, когда предел не существует или равен бесконечности, несобственный интеграл является расходящимся.

Аналогично, если в точке $x=a$ подынтегральная функция $y=f\left( x \right)$ терпит бесконечный разрыв, то несобственный интеграл второго рода определяется равенством:

$\int\limits_{a}^{b}{f\left( x \right)dx}=\underset{\varepsilon \to 0}{\mathop{\lim }}\,\int\limits_{a+\varepsilon }^{b}{f\left( x \right)dx}$

Если подынтегральная функция терпит разрыв в некоторой внутренней точке $c$ отрезка $\left[ a;\ b \right]$ , то несобственный интеграл второго рода определяется формулой:

$\int\limits_{a}^{b}{f\left( x \right)dx}=\int\limits_{a}^{c}{f\left( x \right)dx}+\int\limits_{c}^{b}{f\left( x \right)dx}$

Интеграл, стоящий в левой части равенства, называется сходящимся, если сходятся оба несобственных интеграла в правой части приведенного равенства.

ПРИМЕР 3

Задание

Вычислить интеграл или установить, что он является расходящимся.

$\int\limits_{0}^{1}{\frac{dx}{{{x}^{2}}}}$

Решение

В точке $x=0$ , принадлежащей промежутку интегрирования $\left( 0;\ 1 \right]$ , подынтегральная функция $f\left( x \right)=\frac{1}{{{x}^{2}}}$ терпит разрыв второго рода:

$\underset{x\to 0+0}{\mathop{\lim }}\,f\left( x \right)=\underset{x\to 0+0}{\mathop{\lim }}\,\frac{1}{{{x}^{2}}}\ =\left[ \frac{1}{{{\left( 0+0 \right)}^{2}}}=\frac{1}{+0} \right]=+\infty$

Поэтому рассматриваемый интеграл является несобственным интегралом второго рода, тогда, согласно определению, имеем:

$\int\limits_{0}^{1}{\frac{dx}{{{x}^{2}}}}=\underset{\varepsilon \to 0}{\mathop{\lim }}\,\int\limits_{0+\varepsilon }^{1}{\frac{dx}{{{x}^{2}}}}=\underset{\varepsilon \to 0}{\mathop{\lim }}\,\left. \left( -\frac{1}{x} \right) \right|_{\varepsilon }^{1}=-\underset{\varepsilon \to 0}{\mathop{\lim }}\,\left( 1-\frac{1}{\varepsilon } \right)=-1+\underset{\varepsilon \to 0}{\mathop{\lim }}\,\frac{1}{\varepsilon }=\infty$

а значит, заданный интеграл является расходящимся.