Формулы интегрирования функций

ОПРЕДЕЛЕНИЕ

Функция $F(x)$ называется первообразной функции $f(x) ,$ если выполняется равенство:

${F}'\left( x \right)=f\left( x \right)$

Множество всех первообразных некоторой функции $f(x)$ называется неопределенным интегралом этой функции и обозначается

$\int f(x) dx=F\left( x \right)+C$

где $C$ – произвольная постоянная. Ниже описаны основные свойства и формулы интегрирования функций:

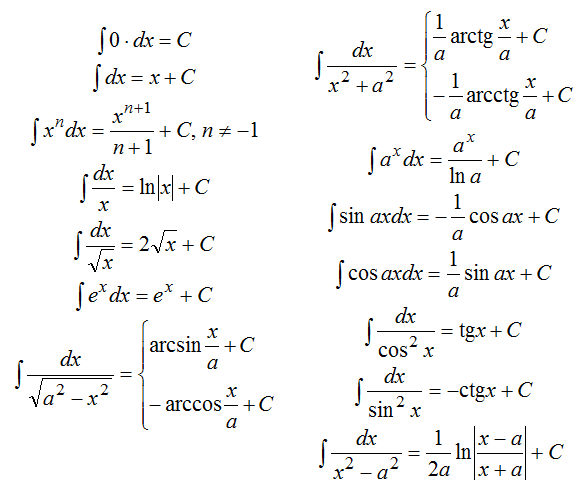
Свойства неопределенного интеграла

Константу можно выносить за знак интеграла:

$\int{c\cdot f\left( x \right)dx}=c\int{f\left( x \right)dx}$

Интеграл суммы/разности двух функций равен сумме/разности интегралов от каждой из них:

$\int{\left[ f\left( x \right)\pm g\left( x \right) \right]dx}=\int{f\left( x \right)dx}\pm \int{g\left( x \right)dx}$

Производная от неопределенного интеграла равна подынтегральной функции:

${{\left( \int{f\left( x \right)dx} \right)}^{\prime }}=f\left( x \right)$

ПРИМЕР 1

Задание

Найти интеграл

$\int{\frac{2\sqrt{x}+x\cos x}{x}dx}$

Решение

Используя правила интегрирования и таблицу интегралов, будем иметь:

$\int{\frac{2\sqrt{x}+x\cos x}{x}dx}=\int{\left( \frac{2\sqrt{x}}{x}+\frac{x\cos x}{x} \right)dx}=\int{\left( \frac{2}{\sqrt{x}}+\cos x \right)dx}=$

$=\int{\frac{2}{\sqrt{x}}dx}+\int{\cos xdx}=2\int{\frac{dx}{\sqrt{x}}}+\sin x=2\cdot 2\sqrt{x}+\sin x+C=4\sqrt{x}+\sin x+C$

Ответ

ПРИМЕР 2

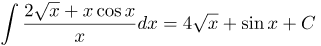Задание

Найти первообразную функции $f\left( x \right)={{x}^{2}}+\sin x-13$

Решение

Искомая первообразная

$\int{f\left( x \right)dx}=\int{\left( {{x}^{2}}+\sin x-13 \right)dx}$

Интеграл от суммы/разности функций равен сумме/разности интегралов от каждой функции, то есть

$\int{\left( {{x}^{2}}+\sin x-13 \right)dx}=\int{{{x}^{2}}dx}+\int{\sin xdx}-\int{13dx}$

Согласно правилам интегрирования и таблице интегралов, имеем:

$\int{\left( {{x}^{2}}+\sin x-13 \right)dx}=\frac{{{x}^{2+1}}}{2+1}+\left( -\cos x \right)-13\int{dx}=\frac{{{x}^{3}}}{3}-\cos x-13x+C$

Ответ

$\frac{{{x}^{3}}}{3}-\cos x-13x+C$

Понравился сайт? Расскажи друзьям!