Примеры интегрирования по частям
Метод интегрирования по частям – один из способов нахождения интегралов. Этот метод применяется тогда, когда подынтегральную функцию можно представить в виде произведения двух функций, одна из которых хорошо дифференцируется, а вторая – интегрируется.
Пусть ![]() и
и ![]() – непрерывные и дифференцируемые функции, тогда справедлива формула
– непрерывные и дифференцируемые функции, тогда справедлива формула
![]()
она называется формулой интегрирования по частям для неопределенного интеграла и
![]()
формула интегрирования по частям для определенного интеграла.
Примеры
| Задание | Найти неопределенный интеграл
|
| Решение | Для нахождения этого интеграла будем использовать метод интегрирования по частям. Положим , при этом можно положить Подставляя все в формулу для интегрирования по частям, получим: |
| Ответ | 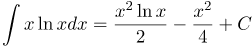 |
| Задание | Найти интеграл
|
| Решение | Найдем этот интеграл, используя метод интегрирования по частям. Обозначим Подставим полученные значения в формулу интегрирования по частям, получим: |
| Ответ | 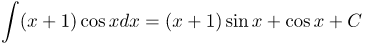 |
| Задание | Найти неопределенный интеграл
|
| Решение | Для нахождения этого интеграла воспользуемся методом интегрирования по частям. Положим
Подставляя все в формулу для интегрирования по частям для неопределенного интеграла, получим: К полученному интегралу Тогда по формуле интегрирования по частям, имеем |
| Ответ | 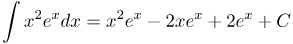 |
| Задание | Вычислить определенный интеграл
|
| Решение | Вычислим этот интеграл, используя метод интегрирования по частям. Положим , будем считать |
| Ответ | 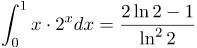 |
| Задание | Вычислить интеграл
|
| Решение | Для вычисления этого интеграла будем использовать метод интегрирования по частям. Положим что
Отметим, что можно считать |
| Ответ | 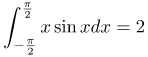 |






![Rendered by QuickLaTeX.com \[ \int _{-\frac{\pi}{2}} ^{\frac{\pi}{2}} x \sin x dx \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-452fb94144932bef92452ebcf28e74bd_l3.png)
![Rendered by QuickLaTeX.com \[ \int _{-\frac{\pi}{2}} ^{\frac{\pi}{2}} x \sin x dx = x (-\cos x) \bigg| _{-\frac{\pi}{2}} ^{\frac{\pi}{2}} - \int _{-\frac{\pi}{2}} ^{\frac{\pi}{2}} (-\cos x) dx = - \left( \frac{\pi}{2} \cos \left( \frac{\pi}{2} \right) - \left( -\frac{\pi}{2} \right) \cos \left( -\frac{\pi}{2} \right) \right) + \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-a1b1f92a78e2cea779a5ea3fbda82508_l3.png)
![Rendered by QuickLaTeX.com \[ + \int _{-\frac{\pi}{2}} ^{\frac{\pi}{2}} \cos x dx = - \left( \frac{\pi}{2} \cdot 0 + \frac{\pi}{2} \cdot 0 \right) + \sin x \bigg| _{-\frac{\pi}{2}} ^{\frac{\pi}{2}} = \sin \left( \frac{\pi}{2} \right) - \sin \left( -\frac{\pi}{2} \right) = 1-(-1)=2 \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-657b595dbd79902c5ab283ddef0855e8_l3.png)





