Метод непосредственного интегрирования

Метод непосредственного интегрирования основан на применении правил интегрирования и использовании табличных интегралов. В простейших примерах для применения этого метода достаточно разложить подынтегральную функцию на слагаемые и постоянные величины вынести за знак интеграла. В некоторых случаях выражение, стоящее под знаком интеграла, можно с помощью алгебраических преобразований упростить так, чтобы можно было применить указанный метод.

ПРИМЕР 1

Задание

Найти интеграл

$\int{\left( 6{{x}^{5}}+\frac{2}{x}-\frac{2}{\sqrt{1-{{x}^{2}}}} \right)dx}$

Решение

Раскладываем заданный интеграл на сумму интегралов:

$\int{\left( 6{{x}^{5}}+\frac{2}{x}-\frac{2}{\sqrt{1-{{x}^{2}}}} \right)dx}=\int{6{{x}^{5}}dx}+\int{\frac{2}{x}dx}-\int{\frac{2}{\sqrt{1-{{x}^{2}}}}dx}$

Константы выносим за знак интеграла:

$\int{\left( 6{{x}^{5}}+\frac{2}{x}-\frac{2}{\sqrt{1-{{x}^{2}}}} \right)dx}=6\int{{{x}^{5}}dx}+2\int{\frac{dx}{x}}-2\int{\frac{dx}{\sqrt{1-{{x}^{2}}}}}$

Далее применяем таблицу интегралов:

$\int{\left( 6{{x}^{5}}+\frac{2}{x}-\frac{2}{\sqrt{1-{{x}^{2}}}} \right)dx}=6\cdot \frac{{{x}^{6}}}{6}+2\cdot \ln \left| x \right|-2\arcsin x+C=$

$={{x}^{6}}+2\cdot \ln \left| x \right|-2\arcsin x+C$

Ответ

ПРИМЕР 2

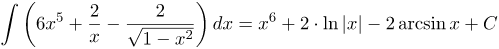Задание

Решить интеграл

$\int{{{\left( {{x}^{2}}+\sqrt{x} \right)}^{2}}dx}$

Решение

Применим к подынтегральной функции формулу сокращенного умножения «квадрат суммы»:

$\int{{{\left( {{x}^{2}}+\sqrt{x} \right)}^{2}}dx}=\int{\left[ {{\left( {{x}^{2}} \right)}^{2}}+2\cdot {{x}^{2}}\cdot \sqrt{x}+{{\left( \sqrt{x} \right)}^{2}} \right]dx}=$

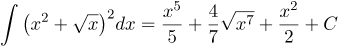$=\int{\left( {{x}^{4}}+2{{x}^{^{\frac{5}{2}}}}+x \right)dx}=\int{{{x}^{4}}dx}+\int{2{{x}^{^{\frac{5}{2}}}}dx}+\int{xdx}=\frac{{{x}^{5}}}{5}+2\cdot \frac{{{x}^{^{\frac{7}{2}}}}}{\frac{7}{2}}+\frac{{{x}^{2}}}{2}+C=$

$=\frac{{{x}^{5}}}{5}+\frac{4}{7}\sqrt{{{x}^{7}}}+\frac{{{x}^{2}}}{2}+C$

Ответ

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Метод непосредственного интегрирования