Свойства неопределенного интеграла
1. Константу можно выносить за знак интеграла:
![]()
| Задание | Найти интеграл |
| Решение | Применим свойство №1:
|
| Ответ | 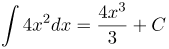 |
2. Интеграл суммы/разности равен сумме/разности интегралов от каждого из слагаемых:
![]()
| Задание | Решить интеграл |
| Решение | Интеграл от суммы равен сумме интегралов:
Каждый из полученных интегралов находим с помощью таблицы интегралов: |
| Ответ | 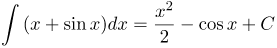 |
3. Производная от интеграла равна подынтегральной функции:
![]()
| Задание | Найти |
| Решение | Согласно свойству имеем, что
|
| Ответ |
4. Интеграл от дифференциала функции равен этой функции плюс постоянная интегрирования:
![]()
| Задание | Решить интеграл |
| Решение | Согласно свойству
|
| Ответ |
5. Если ![]() , то
, то
![]()
| Задание | Известно, что |
| Решение | Согласно свойству делаем вывод, что для |
| Ответ | 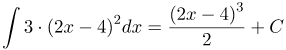 |
6. Интеграл от производной некоторой функции равен этой функции плюс константа интегрирования:
![]()
| Задание | Доказать, что
|
| Доказательство | Найдем интеграл Тогда По свойствам интеграла константу можно выносить за знак интеграла: Применяем таблицу интегралов: Итак, Что и требовалось доказать. |











