Свойства определенного интеграла
- Определенный интеграл не зависит от переменной интегрирования:
![Rendered by QuickLaTeX.com \[\int\limits_{a}^{b}{f\left( x \right)dx}=\int\limits_{a}^{b}{f\left( t \right)dt}=\int\limits_{a}^{b}{f\left( y \right)dy}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-c4656374ba11e8e64b2c550e0dfbc4b0_l3.png)
- Если пределы интегрирования определенного интеграла равны, то такой интеграл равен нулю:
![Rendered by QuickLaTeX.com \[\int\limits_{a}^{a}{f\left( x \right)dx}=0\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-cc59d2f5778a7cd4896bff6b4c97e301_l3.png)
- Если подынтегральная функция
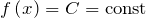 , то определенный интеграл от этой функции по промежутку
, то определенный интеграл от этой функции по промежутку ![Rendered by QuickLaTeX.com \left[ a;\ b \right]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-ddee96308f4557af814c2cf32a05d815_l3.png) равен произведению константы
равен произведению константы 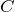 на длину промежутка
на длину промежутка 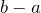 :
:
![Rendered by QuickLaTeX.com \[\int\limits_{a}^{b}{C\cdot dx}=C\left( b-a \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-f53cc1961e6098c2d7e474e2dd16c388_l3.png)
- Постоянный множитель можно выносить за знак определенного интеграла:
![Rendered by QuickLaTeX.com \[\int\limits_{a}^{b}{Cf\left( x \right)dx}=C\int\limits_{a}^{b}{f\left( x \right)dx}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-c0e45b9de9a0d730bf438fada11211b9_l3.png)
- Интеграл от суммы интегрированных на отрезке
![Rendered by QuickLaTeX.com \left[ a;\ b \right]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-ddee96308f4557af814c2cf32a05d815_l3.png) функций равен сумме интегралов от каждой из них:
функций равен сумме интегралов от каждой из них:
![Rendered by QuickLaTeX.com \[\int\limits_{a}^{b}{\left[ {{f}_{1}}\left( x \right)+{{f}_{2}}\left( x \right)+...+{{f}_{n}}\left( x \right) \right]dx}=\int\limits_{a}^{b}{{{f}_{1}}\left( x \right)dx}+\int\limits_{a}^{b}{{{f}_{2}}\left( x \right)dx}+...+\int\limits_{a}^{b}{{{f}_{n}}\left( x \right)dx}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-265c457a2c3b896cd7e20e4d30ced504_l3.png)
- Если в определенном интеграле поменять местами пределы интегрирования, то интеграл поменяет знак на противоположный:
![Rendered by QuickLaTeX.com \[\int\limits_{a}^{b}{f\left( x \right)dx}=-\int\limits_{b}^{a}{f\left( x \right)dx}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-6463114325fbc16a344471046774e909_l3.png)
- Если функция
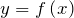 интегрируема на отрезке
интегрируема на отрезке ![Rendered by QuickLaTeX.com \left[ a;\ b \right]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-ddee96308f4557af814c2cf32a05d815_l3.png) , то для
, то для 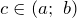 имеет место равенство:
имеет место равенство:
![Rendered by QuickLaTeX.com \[\int\limits_{a}^{b}{f\left( x \right)dx}=\int\limits_{a}^{c}{f\left( x \right)dx}+\int\limits_{c}^{b}{f\left( x \right)dx}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-710aefa289e82ed16f76e0080b763315_l3.png)
- Теорема про среднее. Если функция
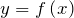 интегрируема на отрезке
интегрируема на отрезке ![Rendered by QuickLaTeX.com \left[ a;\ b \right]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-ddee96308f4557af814c2cf32a05d815_l3.png) , то существует точка
, то существует точка ![Rendered by QuickLaTeX.com \xi \in \left[ a;\ b \right]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-e88237ee6e15a86fa3ede944d2dcb762_l3.png) такая, что имеет место равенство:
такая, что имеет место равенство:
![Rendered by QuickLaTeX.com \[\int\limits_{a}^{b}{f\left( x \right)dx}=f\left( \xi \right)\left( b-a \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-ca1a53e667e3aea259a723337f1c864f_l3.png)
- Если функция
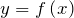 сохраняет знак на некотором промежутке
сохраняет знак на некотором промежутке ![Rendered by QuickLaTeX.com \left[ a;\ b \right]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-ddee96308f4557af814c2cf32a05d815_l3.png) , то определенный интеграл
, то определенный интеграл 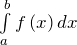 имеет на этом же промежутке тот же знак, что и подынтегральная функция.
имеет на этом же промежутке тот же знак, что и подынтегральная функция. - Если
![Rendered by QuickLaTeX.com {{f}_{1}}\left( x \right)\le {{f}_{2}}\left( x \right),\ x\in \left[ a;\ b \right]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-950a07a119f02ed4d7011027b3d6d3e8_l3.png) , то и
, то и
![Rendered by QuickLaTeX.com \[\int\limits_{a}^{b}{{{f}_{1}}\left( x \right)dx}\le \int\limits_{a}^{b}{{{f}_{2}}\left( x \right)dx}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-627e1f048594abeaa5adf74acd0d7218_l3.png)
- Если функция
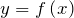 принимает на отрезке
принимает на отрезке ![Rendered by QuickLaTeX.com \left[ a;\ b \right]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-ddee96308f4557af814c2cf32a05d815_l3.png) свои наименьшее
свои наименьшее 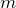 и наибольшее
и наибольшее 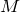 значения, то имеют место неравенства:
значения, то имеют место неравенства:
![Rendered by QuickLaTeX.com \[m\left( b-a \right)\le \int\limits_{a}^{b}{f\left( x \right)dx}\le M\left( b-a \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-aa6fdc519ef65a85b34e7a4e2b2ef7fd_l3.png)
- Модуль определенного интеграла не превосходит интеграл от модуля подынтегральной функции:
![Rendered by QuickLaTeX.com \[\left| \int\limits_{a}^{b}{f\left( x \right)dx} \right|\le \int\limits_{a}^{b}{\left| f\left( x \right) \right|dx}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-854d15748259e2f2b171befe34edb7d6_l3.png)
- Производная от интеграла с переменным верхним пределом равна значению подынтегральной функции от этого предела:
![Rendered by QuickLaTeX.com \[{{\left( \int\limits_{a}^{x}{f\left( t \right)dt} \right)}^{\prime }}=f\left( x \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-ca333d68cd5f28ccad007ac526f5324c_l3.png)
- Пусть функция
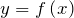 непрерывна на отрезке
непрерывна на отрезке ![Rendered by QuickLaTeX.com \left[ -a;\ a \right]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-99b338e40a0494e6f45e5d5e38c5bb00_l3.png) , симметричном относительно точки
, симметричном относительно точки 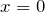 , тогда
, тогда
![Rendered by QuickLaTeX.com \[\int\limits_{-a}^{a}{f\left( x \right)dx}=\left\{ \begin{matrix} & 0,\ f\left( x \right) \\ & 2\int\limits_{0}^{a}{f\left( x \right)dx},\ f\left( x \right) \\ \end{matrix} \right.\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-0a57c597038d5cbb31c83e12ad8f1a5c_l3.png)
где при
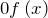 нечётная, а при
нечётная, а при 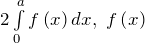 -чётная.
-чётная. - Интеграл от периодической с периодом
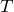 функции
функции 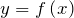 имеет одно и то же значение на любом промежутке длины
имеет одно и то же значение на любом промежутке длины 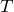 :
:
![Rendered by QuickLaTeX.com \[\int\limits_{0}^{T}{f\left( x \right)dx}=\int\limits_{-T}^{0}{f\left( x \right)dx}=\int\limits_{-\frac{T}{2}}^{\frac{T}{2}}{f\left( x \right)dx}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-2ff7ec904792c19ab88d7278b09e0279_l3.png)











