Определенный интеграл
![Rendered by QuickLaTeX.com \[\int\limits_{a}^{b}{f\left( x \right)dx}=\underset{\Delta {{x}_{i}}\to 0}{\mathop{\lim }}\,\sum\limits_{i=0}^{n}{f\left( {{\xi }_{i}} \right)\Delta {{x}_{i}}}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-e3874a39bd30bb8c8a218f24d633c98b_l3.png)
Например. ![]()
Детальный разбор понятия «Определенный интеграл»
Рассмотрим функцию ![]() , определенную и непрерывную на некотором отрезке
, определенную и непрерывную на некотором отрезке ![]() . Выполним разбиение заданного отрезка с помощью точек
. Выполним разбиение заданного отрезка с помощью точек ![]() на
на ![]() частичных отрезков
частичных отрезков ![]() ,
, ![]() ,…,
,…, ![]() . На каждом частичном отрезке
. На каждом частичном отрезке ![]() выберем произвольную точку
выберем произвольную точку ![]() и вычислим значение
и вычислим значение ![]() заданной функции в ней. Умножим полученное значение на длину
заданной функции в ней. Умножим полученное значение на длину ![]() соответствующего частичного отрезка:
соответствующего частичного отрезка: ![]() . Составим сумму всех таких произведений:
. Составим сумму всех таких произведений:
![Rendered by QuickLaTeX.com \[\sigma =\sum\limits_{i=1}^{n}{f\left( {{\xi }_{i}} \right)\cdot \Delta {{x}_{i}}}=f\left( {{\xi }_{1}} \right)\cdot \Delta {{x}_{1}}+f\left( {{\xi }_{2}} \right)\cdot \Delta {{x}_{2}}+...+f\left( {{\xi }_{n}} \right)\cdot \Delta {{x}_{n}}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-be855444dd608c1800ee1b7ca2349f1e_l3.png)
Такая сумма ![]() называется интегральной суммой функции
называется интегральной суммой функции ![]() на отрезке
на отрезке ![]() .
.
Пусть ![]() – длина наибольшего частичного отрезка:
– длина наибольшего частичного отрезка: ![]() . Если предел
. Если предел ![]() интегральной суммы
интегральной суммы ![]() , когда максимальный диаметр разбиения
, когда максимальный диаметр разбиения ![]() , не зависит ни от способа разбиения отрезка
, не зависит ни от способа разбиения отрезка ![]() на частичные отрезки, ни от выбора точек
на частичные отрезки, ни от выбора точек ![]() в них, то число
в них, то число ![]() называется определенным интегралом от заданной функции
называется определенным интегралом от заданной функции ![]() на отрезке
на отрезке ![]() и обозначается
и обозначается ![]() , то есть
, то есть
![Rendered by QuickLaTeX.com \[\int\limits_{a}^{b}{f\left( x \right)dx}=\underset{d\to 0}{\mathop{\lim }}\,\sum\limits_{i=1}^{n}{f\left( {{\xi }_{i}} \right)\Delta {{x}_{i}}}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-6fa17ab97314d7233bc988d137d84f5d_l3.png)
Здесь числа ![]() и
и ![]() называются соответственно верхним и нижним пределами интегрирования;
называются соответственно верхним и нижним пределами интегрирования; ![]() – подынтегральная функция;
– подынтегральная функция; ![]() – подынтегральное выражение;
– подынтегральное выражение; ![]() – переменная интегрирования;
– переменная интегрирования; ![]() – область или отрезок интегрирования.
– область или отрезок интегрирования.
Примеры решения задач
| Задание | Найти интеграл по определению.
|
| Решение | На отрезке Разобьем отрезок интегрирования и разбиение В качестве Тогда имеем: Выражение, стоящее в числителе дроби, представляет собой сумму геометрической прогрессии, для которой Тогда будем иметь: |
| Ответ | 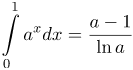 |
Функция ![]() называется интегрируемой на отрезке
называется интегрируемой на отрезке ![]() , если для нее на этом отрезке существует определенный интеграл
, если для нее на этом отрезке существует определенный интеграл ![]() .
.
| Задание | Исследовать функцию |
| Решение | Рассмотрим некоторое разбиение Составляем интегральную сумму Предел этой интегральной суммы Этот предел не зависит ни от разбиения, ни от выбора промежуточных точек, а поэтому функция |
| Ответ | Функция интегрируема. |






![Rendered by QuickLaTeX.com \[ \int\limits_{0}^{1}{{{a}^{x}}dx},\ \left( a>0 \right) \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-9ac2a0af77028ba48602b786ec40a282_l3.png)
![Rendered by QuickLaTeX.com \[ \int\limits_{a}^{b}{f\left( x \right)dx}=\underset{d\to 0}{\mathop{\lim }}\,\sum\limits_{i=1}^{n}{f\left( {{\xi }_{i}} \right)\Delta {{x}_{i}}} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-7a5ea350a24b41a9e8b1edc5a2ae751b_l3.png)
![Rendered by QuickLaTeX.com \[\int\limits_{0}^{1}{{{a}^{x}}dx}=\underset{d=\frac{1}{n}\to 0}{\mathop{\lim }}\,\sum\limits_{i=1}^{n}{f\left( \frac{i}{n} \right)\cdot \frac{1}{n}}\ \left\| \begin{matrix} \frac{1}{n}\to 0\Rightarrow \\ \Rightarrow n\to \infty \\ \end{matrix} \right\|=\underset{n\to \infty }{\mathop{\lim }}\,\frac{1}{n}\sum\limits_{i=1}^{n}{{{a}^{^{\frac{i}{n}}}}}=\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-519d66fc12adb8af66b6ba845e5f4240_l3.png)
![Rendered by QuickLaTeX.com \[=\underset{n\to \infty }{\mathop{\lim }}\,\frac{{{a}^{^{\frac{1}{n}}}}+{{a}^{^{\frac{2}{n}}}}+...+{{a}^{^{\frac{n}{n}}}}}{n}=\underset{n\to \infty }{\mathop{\lim }}\,\frac{{{a}^{\frac{1}{n}}}+{{\left( {{a}^{\frac{1}{n}}} \right)}^{2}}+...+{{\left( {{a}^{\frac{1}{n}}} \right)}^{n}}}{n}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-a02f9ddc174c7d7210e451f15e7b73a5_l3.png)
![Rendered by QuickLaTeX.com \[\int\limits_{0}^{1}{{{a}^{x}}dx}=\underset{n\to \infty }{\mathop{\lim }}\,\frac{{{a}^{\frac{1}{n}}}\left( {{\left( {{a}^{\frac{1}{n}}} \right)}^{n}}-1 \right)}{n\left( {{a}^{\frac{1}{n}}}-1 \right)}=\underset{n\to \infty }{\mathop{\lim }}\,\frac{{{a}^{\frac{1}{n}}}\left( a-1 \right)}{n\left( {{a}^{\frac{1}{n}}}-1 \right)}\ \left\| \begin{matrix} n=\frac{1}{t} \\ t\to 0 \\ \end{matrix} \right\|=\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-20ce6ea9cec810e45a3a958c20c93cfa_l3.png)
![Rendered by QuickLaTeX.com \[\sigma =\sum\limits_{i=1}^{n}{f\left( {{\xi }_{i}} \right)\Delta \,{{x}_{i}}}=\sum\limits_{i=1}^{n}{C\cdot \Delta \,{{x}_{i}}}=C\cdot \sum\limits_{i=1}^{n}{\Delta \,{{x}_{i}}}=C\left( b-a \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-8fea06951635e8eac46f929367e9c885_l3.png)





