Интеграл произведения функций
![]()
В зависимости от того, какие функции стоят под знаком интеграла, интеграл от произведения в некоторых случаях можно выразить через элементарные функции, а в некоторых определенный интеграл произведения функций можно оценить. Для этого используются теоремы про среднее.
Теоремы про среднее
![Rendered by QuickLaTeX.com \[m\int\limits_{a}^{b}{g\left( x \right)dx}\le \int\limits_{a}^{b}{f\left( x \right)g\left( x \right)dx}\le M\int\limits_{a}^{b}{g\left( x \right)dx}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-99b0ce8f1f5a10544618565041230c95_l3.png)
Следствие 1. Пусть функция ![]() интегрируема на отрезке
интегрируема на отрезке ![]() и является ограниченной на этом отрезке:
и является ограниченной на этом отрезке: ![]() Тогда
Тогда
![Rendered by QuickLaTeX.com \[m\left( b-a \right)\le \int\limits_{a}^{b}{f\left( x \right)g\left( x \right)dx}\le M\left( b-a \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-d316d887131c4eb15f6604daa05834ca_l3.png)
![Rendered by QuickLaTeX.com \[\int\limits_{a}^{b}{f\left( x \right)g\left( x \right)dx}=f\left( c \right)\cdot \int\limits_{a}^{b}{g\left( x \right)dx}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-bbed212f543e9361a294d1057bf488bf_l3.png)
Следствие 2. Пусть функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() Тогда существует
Тогда существует ![]() такое, что
такое, что
![Rendered by QuickLaTeX.com \[\int\limits_{a}^{b}{f\left( x \right)g\left( x \right)dx}=f\left( c \right)\left( b-a \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-8a78f8261c037b4a7adcc53dcafaba0b_l3.png)
Примеры решения задач по теме «Интеграл произведения»
| Задание | Оценить интеграл
|
| Решение | Подынтегральная функция или |
| Ответ | 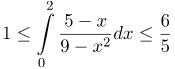 |
| Задание | Оценить интеграл
|
| Решение | Подынтегральная функция Тогда, согласно следствию 1, имеем: или |
| Ответ | 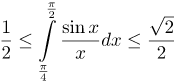 |






![Rendered by QuickLaTeX.com \[ \int\limits_{0}^{2}{\frac{5-x}{9-{{x}^{2}}}dx} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-6d9019ac75b212135782441e65055f1b_l3.png)
![Rendered by QuickLaTeX.com \[\frac{1}{2}\cdot \left( 2-0 \right)\le \int\limits_{0}^{2}{\frac{5-x}{9-{{x}^{2}}}dx}\le \frac{3}{5}\cdot \left( 2-0 \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-5deab3688e1ad96036f64987f1b99018_l3.png)
![Rendered by QuickLaTeX.com \[1\le \int\limits_{0}^{2}{\frac{5-x}{9-{{x}^{2}}}dx}\le \frac{6}{5}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-b7d4e391d131d1a68af97278f0c966a2_l3.png)
![Rendered by QuickLaTeX.com \[ \int\limits_{\frac{\pi }{4}}^{\frac{\pi }{2}}{\frac{\sin x}{x}dx} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-2648ca800bf6702ccadec9bd0b932a22_l3.png)
![Rendered by QuickLaTeX.com \[\frac{2}{\pi }\cdot \left( \frac{\pi }{2}-\frac{\pi }{4} \right)\le \int\limits_{\frac{\pi }{4}}^{\frac{\pi }{2}}{\frac{\sin x}{x}dx}\le \frac{2\sqrt{2}}{\pi }\cdot \left( \frac{\pi }{2}-\frac{\pi }{4} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-6d5921fe169c46690cac5ebaf9186247_l3.png)
![Rendered by QuickLaTeX.com \[\frac{2}{\pi }\cdot \frac{\pi }{4}\le \int\limits_{\frac{\pi }{4}}^{\frac{\pi }{2}}{\frac{\sin x}{x}dx}\le \frac{2\sqrt{2}}{\pi }\cdot \frac{\pi }{4} \text{ } \Rightarrow \text{ } \frac{1}{2}\le \int\limits_{\frac{\pi }{4}}^{\frac{\pi }{2}}{\frac{\sin x}{x}dx}\le \frac{\sqrt{2}}{2}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-1163f082b7535a3eff6937b785465262_l3.png)





