Свойства матриц
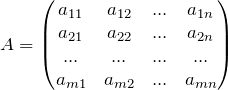 называется прямоугольная таблица чисел, состоящая из
называется прямоугольная таблица чисел, состоящая из Она имеет размер ![]() и обозначается
и обозначается ![]() .
.
Элементы матрицы А обозначают буквами с двумя индексами, первый из которых указывает номер строки, в которой стоит элемент, а второй – номер столбца.
Две матрицы А и В называются равными, если они имеют одинаковый размер и их соответствующие элементы равны, т.е.
![Rendered by QuickLaTeX.com \[{{A}_{m\times n}}={{B}_{k\times p}}\Leftrightarrow \left\{ \begin{array}{*{35}{l}} m=k\,, \\ n=p\,, \\ a_{ij}=b_{ij}\,,\,\,\,i=\overline{1,m},\,\,j=\overline{1,n}\,. \\ \end{array} \right.\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-258bc435b76623b72ae044d3cbc9f0b7_l3.png)
Суммой двух матриц А и В одинакового размера ![]() называется матрица С того же размера, элементы которой равны сумме соответствующих элементов матриц-слагаемых, т.е. если
называется матрица С того же размера, элементы которой равны сумме соответствующих элементов матриц-слагаемых, т.е. если ![]() и
и ![]() , то
, то
![]()
где ![]()
Произведением матрицы ![]() на число
на число ![]() называется матрица того же размера
называется матрица того же размера ![]() , каждый элемент которой получен умножением соответствующего элемента матрицы
, каждый элемент которой получен умножением соответствующего элемента матрицы ![]() на число
на число ![]() , т.е.
, т.е.
![]()
где ![]()
Свойства линейных операций над матрицами
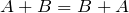 – коммутативность (переместительный закон) сложения;
– коммутативность (переместительный закон) сложения;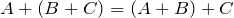 – ассоциативность (сочетательный закон) сложения;
– ассоциативность (сочетательный закон) сложения;- для любой матрицы А существует единственная нулевая матрица
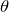 такая, что
такая, что 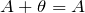 ;
; - для любой матрицы А существует единственная матрица
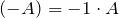 , называемая противоположной, такая что
, называемая противоположной, такая что 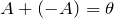 , где
, где 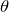 – нулевая матрица;
– нулевая матрица; 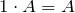 ;
;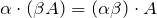 ;
;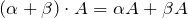 ;
;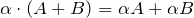 .
.
| Задание | Для матриц |
| Решение | Найдем матрицы Далее найдем их сумму |
| Ответ | 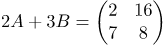 |
Произведением матрицы А размера ![]() на матрицу В размера
на матрицу В размера ![]() называется матрица
называется матрица ![]() размера
размера ![]() , элемент
, элемент ![]() которой, стоящий в
которой, стоящий в ![]() -й строке и в
-й строке и в ![]() -м столбце, равен сумме произведений соответствующих элементов
-м столбце, равен сумме произведений соответствующих элементов ![]() -й строки матрицы A и
-й строки матрицы A и ![]() -го столбца матрицы В:
-го столбца матрицы В:
![Rendered by QuickLaTeX.com \[c_{ij}=a_{i1}\cdot b_{1j}+a_{i2}\cdot b_{2j}+...+a_{in}\cdot b_{nk}=\sum\limits_{p=1}^{n}{a_{ip}b_{pk}}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-b984cbf70f30ebf0f8cb1bc35bcc97c2_l3.png)
Замечание. Для матриц А и В произведение определено, если число столбцов матрицы А равно числу строк матрицы В.
Свойства операции умножения матриц
![]() – матрицы,
– матрицы, ![]()
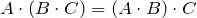 – ассоциативность умножения;
– ассоциативность умножения;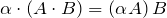 ;
;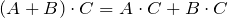 ;
;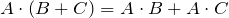 ;
;- Если матрица
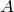 имеет размер
имеет размер 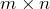 , то равенство
, то равенство 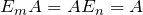 справедливо, только если
справедливо, только если 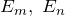 – единичные матрицы
– единичные матрицы 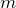 -го и
-го и 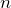 -го порядка.
-го порядка.
| Задание | Найти произведение матриц
|
| Решение | Матрица |
| Ответ | 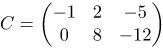 |
Матрица ![]() размера
размера ![]() называется транспонированной к матрице
называется транспонированной к матрице ![]() размера
размера ![]() , если в ней на месте
, если в ней на месте ![]() стоит элемент
стоит элемент ![]() матрицы
матрицы ![]() , или, иначе, матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером. Таким образом, если
, или, иначе, матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером. Таким образом, если
![Rendered by QuickLaTeX.com \[A=\left( \begin{matrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ ... & ... & ... & ... \\ a_{m1} & a_{m2} & ... & a_{mn} \\ \end{matrix} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-9afb5787bebd038d613e77266bc3f3a6_l3.png)
то
![Rendered by QuickLaTeX.com \[{{A}^{t}}=\left( \begin{matrix} a_{11} & a_{21} & ... & a_{m1} \\ a_{12} & a_{22} & ... & a_{m2} \\ ... & ... & ... & ... \\ a_{1n} & a_{2n} & ... & a_{mn} \\ \end{matrix} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-e4d8a091b6f8bd8ae00b71c1a0ae1fd8_l3.png)
Свойства операции транспонирования матриц
![]() – матрицы,
– матрицы, ![]() ):
):
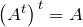 ;
;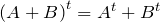 ;
;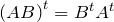 ;
;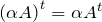 .
.






![Rendered by QuickLaTeX.com \[\begin{matrix} {{C}_{2\times 3}}=\left( \begin{matrix} -1 & 2 \\ 0 & 4 \\ \end{matrix} \right)\cdot \left( \begin{matrix} 1 & 2 & -1 \\ 0 & 2 & -3 \\ \end{matrix} \right)=\left( \begin{matrix} -1\cdot 1+2\cdot 0 & -1\cdot 2+2\cdot 2 & -1\cdot \left( -1 \right)+2\cdot (-3) \\ 0\cdot 1+4\cdot 0 & 0\cdot 2+4\cdot 2 & 0\cdot \left( -1 \right)+4\cdot (-3) \\ \end{matrix} \right)= \\ =\left( \begin{matrix} -1 & 2 & -5 \\ 0 & 8 & -12 \\ \end{matrix} \right) \\ \end{matrix}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-47fb18adb1070c698649ca30c48722e8_l3.png)





