Транспонирование матрицы

Транспонирование это одна из операций над матрицами, которая заключается в том, что строки исходной матрицы $A$ записывают в новую матрицу по столбцам. Полученную таким образом матрицу называют транспонированной матрицей $A$ и обозначают ${{A}^{T}} .$

ПРИМЕР 1

Задание	Транспонировать матрицы $A$ и $B$ $A =\left( 1\quad -2\quad 0\quad 4 \right) \text{ }\text{ },\text{ }\text{ } B =\left( \begin{matrix} 2 & 0 \\ -3 & 1 \\ \end{matrix} \right)$
Ответ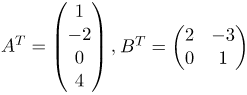

Свойства транспонирования матриц

дважды транспонированная матрица равна исходной матрице
${{A}^{TT}}={{\left( {{A}^{T}} \right)}^{T}}=A$
транспонированная матрица суммы равна сумме транспонированных матриц
${{\left( A + B \right)}^{T}}={{A}^{T}}+{{B}^{T}}$
транспонированная матрица произведения равна произведению транспонированных матриц сомножителей, взятых в обратном порядке
${{\left( A \cdot B \right)}^{T}}={{A}^{T}}\cdot {{B}^{T}}$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Транспонирование матрицы

Свойства транспонирования матриц