Виды матриц
Пусть матрица ![]() состоит из
состоит из ![]() строк и
строк и ![]() столбцов
столбцов ![]() . В зависимости от чисел
. В зависимости от чисел ![]() и
и ![]() матрицы делятся на:
матрицы делятся на:
- квадратные, если
 :
:
![Rendered by QuickLaTeX.com \[A=\left( \begin{matrix} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \ldots & \ldots & \ldots & \ldots \\ a_{n1} & a_{n2} & \ldots & a_{nn} \\ \end{matrix} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-4a74f124f136b62f586e392579e74eda_l3.png)
Подробнее про квадратные матрицы читайте по ссылке.
- прямоугольные, если
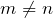 :
:
![Rendered by QuickLaTeX.com \[A=\left( \begin{matrix} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \ldots & \ldots & \ldots & \ldots \\ a_{m1} & a_{m2} & \ldots & a_{mn} \\ \end{matrix} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-87b32515a5b0178e5b343e67147fc0d8_l3.png)
- вектор-строка, если
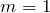 (матрица типа
(матрица типа 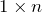 ):
):
![Rendered by QuickLaTeX.com \[A=\left( \begin{matrix} a_{11} & a_{12} & \ldots & a_{1n} \\ \end{matrix} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-83a93fffea50cf09b37a20547a4e517c_l3.png)
- вектор-столбец, если
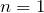 (матрица типа
(матрица типа 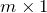 ):
):
![Rendered by QuickLaTeX.com \[A=\left( \begin{matrix} a_{11} \\ a_{21} \\ \vdots \\ a_{m1} \\ \end{matrix} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-b3ad7be187931555c2b713ff4b6ebd2c_l3.png)
- скаляр, если матрица имеет размерность
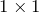 :
:
![Rendered by QuickLaTeX.com \[A=\left( a_{11} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-c2ed433b2e94a0195b140b00ba28696c_l3.png)
В зависимости от вида и распределения элементов в матрице выделяют следующие типы матриц:
- нулевая матрица – матрица, все элементы которой нули, обозначается
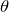 :
:
![Rendered by QuickLaTeX.com \[\theta =\left( \begin{matrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{matrix} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-6d7f2f5a8b5ef5215d7a940f3a83097f_l3.png)
- диагональная матрица – квадратная матрица, все элементы которой, кроме диагональных
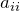 , равны 0:
, равны 0:
![Rendered by QuickLaTeX.com \[A=\left( \begin{matrix} 1 & 0 & 0 \\ 0 & 4 & 0 \\ 0 & 0 & -2 \\ \end{matrix} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-74f0d6b95e59a82b73af273d939e70d2_l3.png)
Подробнее про диагональные матрицы читайте по ссылке.
- скалярная матрица – диагональная матрица, у которой элементы главной диагонали равны:
![Rendered by QuickLaTeX.com \[A=\left( \begin{matrix} a & 0 & \ldots & 0 \\ 0 & a & \ldots & 0 \\ \ldots & \ldots & \ldots & \ldots \\ 0 & 0 & \ldots & a \\ \end{matrix} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-eac1aae8561c1a8a1f70adee6b92697b_l3.png)
- единичная матрица – скалярная матрица, у которой все диагональные элементы равны 1. Обозначается
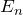 :
:
![Rendered by QuickLaTeX.com \[{{E}_{3}=\left( \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-adeb540d0cb05d74610ad1b244a30aa3_l3.png)
Подробнее про единичные матрицы читайте по ссылке.
- треугольная матрица – матрица, в которой ниже (нижняя треугольная) или выше (верхняя треугольная) главной диагонали все элементы нулевые:
![Rendered by QuickLaTeX.com \[B=\left( \begin{matrix} 1 & 2 & -3 \\ 0 & 2 & 5 \\ 0 & 0 & -1 \\ \end{matrix} \right); \qquad C=\left( \begin{matrix} 3 & 0 & 0 \\ 2 & 4 & 0 \\ 8 & -1 & -5 \\ \end{matrix} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-da03d53e6aab109a0bd94af0dccbbeab_l3.png)











