Матрицы: основные понятия и определения
Матрицей называется прямоугольная таблица чисел. Элементы матрицы можно занумеровать, тогда элемент матрицы ![]() будет находиться на пересечении
будет находиться на пересечении ![]() -той строки и
-той строки и ![]() -того столбца. Матрица, состоящая из
-того столбца. Матрица, состоящая из ![]() строк и
строк и ![]() столбцов, имеет вид
столбцов, имеет вид
![Rendered by QuickLaTeX.com \[\left( \begin{matrix} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \ldots & \ldots & \ldots & \ldots \\ a_{m1} & a_{m2} & \ldots & a_{mn} \\ \end{matrix} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-e4a59364bced5228524f62a96c249ddc_l3.png)
При этом говорят, что эта матрица имеет размер ![]() .
.
Способы обозначения матриц
Матрицы обозначают:
- круглыми скобками или двойными вертикальными линиями
- большими буквами
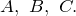
- сокращенно
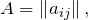
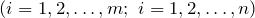 или
или 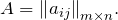
![Rendered by QuickLaTeX.com \[\left( \begin{matrix} 1 & 2 & 1 \\ 0 & 4 & 2 \\ -1 & 3 & 1 \\ \end{matrix} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-524e32fb6fd1b7590c015b0deffccfa6_l3.png)
![Rendered by QuickLaTeX.com \[\left\| \begin{matrix} 1 & 2 & 1 \\ 0 & 4 & 2 \\ -1 & 3 & 1 \\ \end{matrix} \right\|\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-50c15b0822e6176f7ad80f75ecb6b98d_l3.png)
Виды матриц
В зависимости от размера матрицы, вида и размещения элементов выделяют такие виды матриц:
- если число строк и столбцов в матрице совпадает и равно
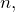 то такая матрица называется квадратной порядка
то такая матрица называется квадратной порядка 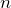 ;
; - если число строк не совпадает с числом столбцов, то матрица называется прямоугольной;
- если матрица состоит из одной строки, то её называют вектор-строка;
- если матрица состоит из одного столбца, то её называют вектор-столбец;
- матрицу размером
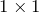 называют скаляром;
называют скаляром; - если все элементы квадратной матрицы, кроме элементов
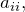 стоящих на главной диагонали, равны нулю, то такая матрица называется диагональной:
стоящих на главной диагонали, равны нулю, то такая матрица называется диагональной: - диагональная матрица, у которой все элементы главной диагонали – единицы, называется единичной и обозначается буквой
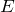
- если все элементы матрицы нули, то её называют нулевой матрицей;
- квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю, называется треугольной. Если нули расположены ниже главной диагонали, то матрица верхнетреугольная, а если выше – нижнетреугольная.
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[D=\left( \begin{matrix} 1 \\ 2 \\ 0 \\ \end{matrix} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-ba4c2083fe6a7ea97c884a1582ea0743_l3.png)
![]()
![Rendered by QuickLaTeX.com \[M=\left( \begin{matrix} -1 & 0 & 0 \\ 0 & 4 & 0 \\ 0 & 0 & 2 \\ \end{matrix} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-7e8f9b3b01100d298ac5a2cd39961bda_l3.png)
![Rendered by QuickLaTeX.com \[E=\left( \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-2deb0a1c0b7762fea8ff7539599318ca_l3.png)
Равные матрицы
Две матрицы ![]() и
и ![]() равны, если
равны, если
- обе они имеют одинаковый размер;
- их соответствующие элементы равны.











