Внесение под знак дифференциала
При сведении заданного интеграла к табличному часто используются следующие преобразования дифференциала как операция «подведения под знак дифференциала». При этом используется формула:
![]()
Вообще говоря, внесение (подведение) под знак дифференциала и замена переменной (метод подстановки) – это один и тот же метод нахождения неопределенного интеграла; отличие состоит только в оформлении.
Суть метода
Итак, внесение под знак интеграла опирается на следующее правило интегрирования. Если в произведении функции, стоящей под знаком интеграла, и дифференциала можно увидеть произведение другой функции и дифференциала от нее, то применяем подведение под знак дифференциала, то есть если
![Rendered by QuickLaTeX.com \[\begin{cases} \int{f\left( \phi \left( x \right) \right)\cdot {\phi }'\left( x \right)dx} \\ u=\phi \left( x \right) \\ \end{cases} \right.\Rightarrow \int{f\left( \phi \left( x \right) \right)\cdot {\phi }'\left( x \right)dx}=\int{f\left( u \right)du}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-c9c0ead11370e819c2f75beb68efd1f7_l3.png)
При внесении под знак дифференциала необходимо иметь в виду простейшие преобразования дифференциала:
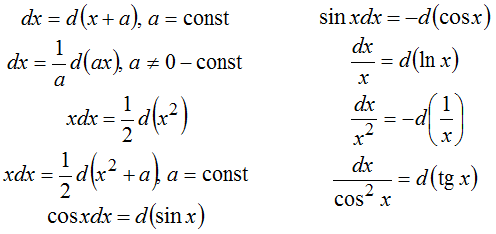
Очень часто метод внесения под знак дифференциала используют для нахождения интегралов вида
![]()
Поэтому имеют место следующие формулы для неопределенных интегралов:
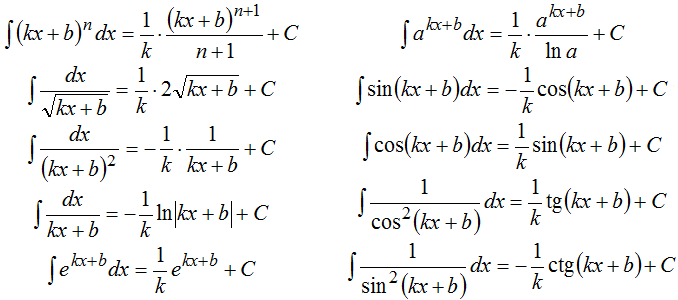
Примеры внесения под знак дифференциала
| Задание | Найти интеграл
|
| Решение | Внесем выражение, стоящее в знаменателе, под знак дифференциала:
|
| Ответ | 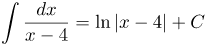 |
| Задание | Решить интеграл |
| Решение | Внесем основание степени под дифференциал:
|
| Ответ | 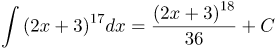 |











