Методы решения интегралов

1. Непосредственное интегрирование

Непосредственное интегрирование – метод интегрирования, при котором подынтегральная функция путем тождественных преобразований и применения свойств интеграла приводится к одному или нескольким табличным интегралам.

ПРИМЕР 1

Задание

Найти интеграл

$\int{\frac{{{x}^{2}}+x\sin x}{x}dx}$

Решение

Почленно поделим подынтегральную функцию:

$\int{\frac{{{x}^{2}}+x\sin x}{x}dx}=\int{\left( \frac{{{x}^{2}}}{x}+\frac{x\sin x}{x} \right)dx}=\int{\left( x+\sin x \right)dx}$

Интеграл от суммы равен сумме интегралов:

$\int{\frac{{{x}^{2}}+x\sin x}{x}dx}=\int{xdx}+\int{\sin xdx}$

Получили сумму табличных интегралов, поэтому имеем:

$\int{\frac{{{x}^{2}}+x\sin x}{x}dx}=\frac{{{x}^{2}}}{2}-\cos x+C$

Ответ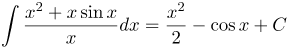

Подробнее про непосредственное интегрирование читайте по ссылке.

2. Метод подведения под знак дифференциала

Метод подведения под знак дифференциала. Этот метод является эквивалентным методу подстановки. Если $f\left( x \right)=v\left( u\left( x \right) \right)$ , то

$\int{f\left( x \right)dx}=\int{v\left( u\left( x \right) \right)}dx\cdot \frac{d\left( u\left( x \right) \right)}{d\left( u\left( x \right) \right)}=\int{v\left( u\left( x \right) \right)}\cdot \frac{d\left( u\left( x \right) \right)}{\frac{d\left( u\left( x \right) \right)}{dx}}=\int{v\left( u\left( x \right) \right)}\cdot \frac{d\left( u\left( x \right) \right)}{{u}'\left( x \right)}$

ПРИМЕР 2

Задание

Решить интеграл $\int{x\sin {{x}^{2}}dx}$

Решение

Внесем $x$ под знак дифференциала:

$xdx=d\left( \frac{{{x}^{2}}}{2} \right)=\frac{1}{2}d\left( {{x}^{2}} \right)$

Тогда будем иметь:

$\int{x\sin {{x}^{2}}dx}=\int{\sin {{x}^{2}}\cdot \frac{1}{2}d\left( {{x}^{2}} \right)}=\frac{1}{2}\int{\sin {{x}^{2}}d\left( {{x}^{2}} \right)}$

Согласно таблице интегралов

$\int{\sin {t}dt}=-\cos t+C$

Тогда при $t={{x}^{2}}$ имеем:

$\int{x\sin {{x}^{2}}dx}=\frac{1}{2}\int{\sin {{x}^{2}}d\left( {{x}^{2}} \right)}=\frac{1}{2}\cdot \left( -\cos {{x}^{2}} \right)+C=-\frac{\cos {{x}^{2}}}{2}+C$

Ответ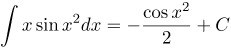

Подробнее про метод подведения под знак дифференциала читайте по ссылке.

3. Метод замены переменной или метод подстановки

Метод замены переменной или метод подстановки. Этот метод заключается во введении новой переменной интегрирования (то есть делается подстановка). При этом заданный интеграл приводится к новому интегралу, который является табличным или с помощью преобразований его можно свести к табличному.

Пусть требуется вычислить интеграл $\int{f\left( x \right)dx}$ . Сделаем подстановку $x=\phi \left( t \right)$ . Тогда $dx={\phi }'\left( t \right)dt$ и интеграл принимает вид:

$\int{f\left( x \right)dx}=\int{f\left( \phi \left( t \right) \right)\cdot {\phi }'\left( t \right)dt}$

ПРИМЕР 3

Задание

Найти интеграл

$\int{\frac{\ln x}{x}dx}$

Решение

Как видим под знаком интеграла стоит функция $f\left( x \right)=\ln x$ и ее производная ${f}'\left( x \right)={{\left( \ln x \right)}^{\prime }}=\frac{1}{x}$ . Тогда делаем замену переменных $\ln x=t$ , тогда дифференциал $\frac{dx}{x}=dt$ .

Итак, интеграл принимает вид:

$\int{\frac{\ln x}{x}dx}=\int{\ln x\cdot \frac{dx}{x}}=\int{tdt}=\frac{{{t}^{2}}}{2}+C$

Неопределенный интеграл зависит от переменной интегрирования, поэтому делаем обратную замену $t=\ln x$ :

$\int{\frac{\ln x}{x}dx}=\frac{{{\ln }^{2}}x}{2}+C$

Ответ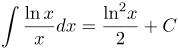

Подробнее про метод замены переменной/подстановки читайте по ссылке.

4. Метод интегрирования по частям

Метод интегрирования по частям. Этот метод основывается на следующей формуле:

$\int{udv}=uv-\int{vdu}$

или

$\int{u\left( x \right){v}'\left( x \right)dx}=u\left( x \right)v\left( x \right)-\int{v\left( x \right){u}'\left( x \right)dx}$

При этом предполагается, что нахождение интеграла $\int{vdu}$ проще, чем исходного интеграла $\int{udv}$ . В противном случае применение метода неоправданно.

ПРИМЕР 4

Задание

Решить интеграл $\int{x\sin xdx}$

Решение

Применим метод интегрирования по частям:

$\int{x\sin xdx}\ \left\| \begin{matrix} u=x & dv=\sin xdx \\ du=dx & v=-\cos x \\ \end{matrix} \right\|=x\cdot \left( -\cos x \right)-\int{\left( -\cos x \right)dx}=$

$=-x\cos x+\int{\cos xdx}=-x\cos x+\sin x+C$

Ответ

$\int{x\sin xdx}=-x\cos x+\sin x+C$

Подробнее про метод интегрирования по частям читайте по ссылке.

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Методы решения интегралов

1. Непосредственное интегрирование

2. Метод подведения под знак дифференциала

3. Метод замены переменной или метод подстановки

4. Метод интегрирования по частям