Интегрирование по частям
Интегрирование по частям – один из способов нахождения интеграла. Суть метода состоит в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных функций в месте со своей производной (каждая из которых может быть как элементарной функцией, так и композицией элементарных), то справедлива следующая формула:
![Rendered by QuickLaTeX.com \[ \int{udv}=uv-\int{vdu} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-7cd0dd32963e4ab90525320143d0fcb8_l3.png)
которая называется формулой интегрирования по частям.
Доказательство формулы интегрирования по частям
Доказательство. Для дифференциала произведения двух непрерывных вместе со своими производными функций имеет место равенство:
![]()
Проинтегрируем последнее равенство:
![]()
По свойствам интегралов имеем:
![]()
Или, если переписать в ином виде, имеем:
![]()
Что и требовалось доказать.
Итак, интегрирование по частям состоит в том, что подынтегральное выражение заданного интеграла представляется каким-либо образом в виде произведения двух сомножителей ![]() и
и ![]() (это зачастую можно осуществить несколькими способами); затем, после нахождения
(это зачастую можно осуществить несколькими способами); затем, после нахождения ![]() (находится из
(находится из ![]() интегрированием) и
интегрированием) и ![]() (дифференцируют выражение для
(дифференцируют выражение для ![]() ), используется формула интегрирования по частям.
), используется формула интегрирования по частям.
Для каких типов интегралов используют формулу
Некоторые типы интегралов, которые удобно вычислять методом интегрирования по частям.
- Интегралы вида
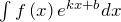 ,
, 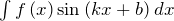 ,
, 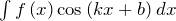 .
.
Здесь
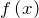 – многочлен. В данном случае
– многочлен. В данном случае 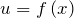 , а в качестве
, а в качестве 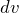 взять все остальные сомножители в подынтегральной функции.
взять все остальные сомножители в подынтегральной функции. - Интегралы вида
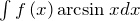 ,
, 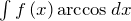 ,
, 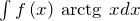 ,
, 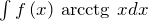 ,
, 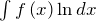 .
.
Здесь нужно взять
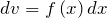 , а тогда
, а тогда 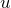 – все остальные сомножители.
– все остальные сомножители. - Интегралы вида
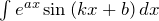 ,
, 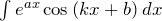 .
.
За
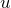 можно принять функцию
можно принять функцию 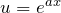 .
.
Примеры решения задач
| Задание | Найти интеграл |
| Решение | В качестве |
| Ответ | 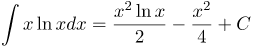 |
| Задание | Решить интеграл |
| Решение | В качестве Получили интеграл, который находится методом интегрирования по частям. Поэтому снова его применяем. Здесь опять в качестве Итак, пришли к исходному интегралу. Запишем интегральное равенство (в последней серии формул подчеркнутые выражения): Решая записанное равенство относительно неизвестного интеграла, будем иметь: Добавляем еще константу интегрирования и окончательно имеем: |
| Ответ | 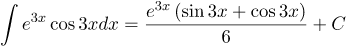 |











