Метод неопределенных коэффициентов
Метод неопределенных коэффициентов применяют при интегрировании рациональных дробей.
Любая правильная рациональная дробь ![]() может быть единственным образом представлена в виде суммы простых рациональных дробей.
может быть единственным образом представлена в виде суммы простых рациональных дробей.
Простыми (наипростейшими) рациональными дробями называются дроби вида:
![]()
причем квадратный трехчлен ![]() не имеет действительных корней (то есть
не имеет действительных корней (то есть ![]() );
);
![]()
Если заданная рациональная дробь неправильная, то вначале нужно выделить целую часть, а для этого поделить числитель на знаменатель в столбик.
| Задание | Выполнить деление многочлена |
| Решение | Поделим многочлен 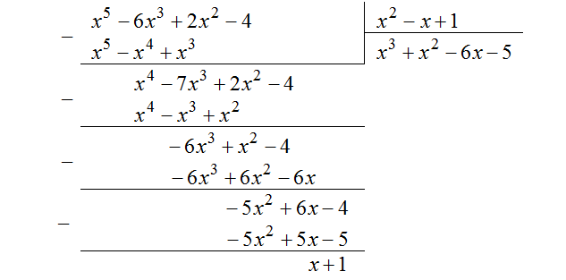
То есть |
| Ответ | 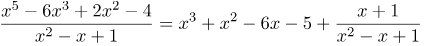 |
Алгоритм метода неопределенных коэффициентов
Чтобы разложить правильную рациональную дробь ![]() на простые дроби, необходимы следующие действия.
на простые дроби, необходимы следующие действия.
- Разложить знаменатель
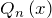 на линейные и квадратные множители, не имеющие действительных корней (см. знаменатели простейших рациональных дробей). Каждому сомножителю вида
на линейные и квадратные множители, не имеющие действительных корней (см. знаменатели простейших рациональных дробей). Каждому сомножителю вида 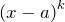 разложения
разложения 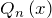 отвечает в разложении дроби
отвечает в разложении дроби 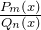 выражение вида
выражение вида
![Rendered by QuickLaTeX.com \[\frac{A_{1}}{x-a}+\frac{A_{2}}{{{\left( x-a \right)}^{2}}}+...+\frac{A_{k}}{{{\left( x-a \right)}^{k}}}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-b695ac818e8f7102b789be2c80d875c9_l3.png)
А каждому сомножителю
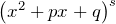 отвечает выражение вида
отвечает выражение вида![Rendered by QuickLaTeX.com \[\frac{B_{1}x+C_{1}}{x^{2}+px+q}+\frac{B_{2}x+C_{2}}{{{\left( x^{2}+px+q \right)}^{2}}}+...+\frac{B_{s}x+C_{s}}{{{\left( x^{2}+px+q \right)}^{s}}}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-b8f70b993b81b7ccbb7af9a4272339cf_l3.png)
- Записать разложение
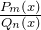 на простейшие дроби с неизвестными коэффициентами, используя приведенные выше разложения. Отметим, что коэффициенты разложений пока являются неизвестными.
на простейшие дроби с неизвестными коэффициентами, используя приведенные выше разложения. Отметим, что коэффициенты разложений пока являются неизвестными. - Сумму простейших дробей привести к общему знаменателю.
- Далее используется тот факт, что две дроби равны, если равны их числители, и равны их знаменатели соответственно. Поэтому приравниваем числитель исходной дроби
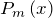 и дроби, которая получилась в пункте 3.
и дроби, которая получилась в пункте 3. - Два многочлена равны, когда равны коэффициенты при соответствующих степенях переменной. Согласно чему получаем систему уравнений относительно неопределенных коэффициентов.
- Решив эту систему, определим коэффициенты и запишем разложение дроби
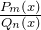 на простые дроби.
на простые дроби.
| Задание | Представить дробь в виде суммы простейших дробей.
|
| Решение | Заданная дробь является правильной, так как степень числителя меньше степени знаменателя. Поэтому раскладываем знаменатель Тогда искомое разложение принимает вид: В правой части приводим к общему знаменателю: Две дроби равны, если равны их числители и знаменатели соответственно, то есть получаем Два многочлена равны, если равны коэффициенты при соответствующей степени переменной: Решая полученную систему относительно неизвестных коэффициентов Итак, искомое представление в виде суммы простейших дробей |
| Ответ | 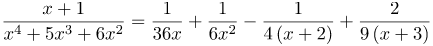 |
Примеры решения интегралов данным методом
| Задание | Найти интеграл
|
| Решение | Подынтегральная функция 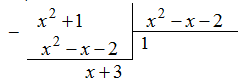
То есть Дробь Неизвестные коэффициенты Далее воспользуемся тем фактом, что две дроби равны, если равны коэффициенты при соответствующих степенях. В итоге получаем равенство двух многочленов: Два многочлена равны, если равны коэффициенты при соответствующих степенях: То есть Тогда заданный интеграл принимает вид: |
| Ответ | 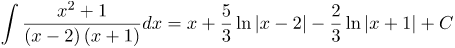 |






![Rendered by QuickLaTeX.com \[\left. \begin{matrix} & x^{3} \\ & x^{2} \\ & x^{1} \\ & x^{0} \\ \end{matrix} \right|\begin{array}{lcl} A_{1}+A_{3}+A_{4}=0, \\ 5A_{1}+A_{2}+3A_{3}+2A_{4}=0, \\ 6A_{1}+5A_{2}=1, \\ 6A_{2}=1. \\ \end{array}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-b7d6c9cb73927b23d2c58db0ddf065b9_l3.png)
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{lcl} A_{1}+A_{3}+A_{4}=0, \\ 5A_{1}+A_{2}+3A_{3}+2A_{4}=0, \\ 6A_{1}+5A_{2}=1, \\ 6A_{2}=1 \\ \end{array} \right\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-49ba98142edae03de34bed2d6874a5e0_l3.png)
![Rendered by QuickLaTeX.com \[\left\{ \begin{matrix} A_{1}=\frac{1}{36}, \\ A_{2}=\frac{1}{6}, \\ A_{3}=-\frac{1}{4}, \\ A_{4}=\frac{2}{9}. \\ \end{matrix} \right.\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-b0186678d0e2671cde04f06754c94f66_l3.png)





