Примеры решения неопределенных интегралов
Теория про неопределенные интегралы
![]()
При нахождении неопределенных интегралов подынтегральную функцию сводят к одной из табличных функций. Если подынтегральная функция ![]() не может быть непосредственно преобразована к одной из табличных функций, то можно использовать метод внесения под дифференциал, метод замены переменной или интегрирование по частям.
не может быть непосредственно преобразована к одной из табличных функций, то можно использовать метод внесения под дифференциал, метод замены переменной или интегрирование по частям.
Примеры
| Задание | Найти неопределенный интеграл
|
| Решение | Используя свойство интегралов, заменим интеграл суммы суммой интегралов и вынесем коэффициенты за знак интеграла:
Далее преобразуем степени переменных: Применяя таблицу интегралов, получим: |
| Ответ | 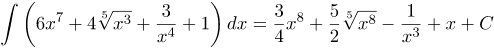 |
| Задание | Найти неопределенный интеграл
|
| Решение | Преобразуем сумму в числителе следующим образом:
Разобьем последний интеграл на сумму двух интегралов, разделив почленно числитель на знаменатель: Последние два интеграла являются табличными, а тогда будем иметь: |
| Ответ | 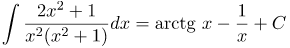 |
| Задание | Найти неопределенный интеграл
|
| Решение | Вынесем общую степень Последний интеграл является табличным интегралом от показательной функции и равен |
| Ответ | 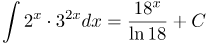 |
| Задание | Найти неопределенный интеграл
|
| Решение | Данный интеграл не выражается в табличных функциях, но если рассмотреть вместо переменной выражение Рассматривая последний интеграл как интеграл от степенной функции, будем иметь: |
| Ответ | 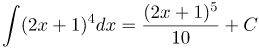 |
| Задание | Найти неопределенный интеграл
|
| Решение | Заданный интеграл нельзя преобразовать элементарными преобразования к табличному интегралу. Для его нахождения воспользуемся методом замены переменной. Введем замену Подставляя, введенную замену, в исходный интеграл получим: Сделаем обратную замену |
| Ответ | 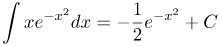 |






![Rendered by QuickLaTeX.com \[ = 6 \cdot \frac{x^{7+1}}{7+1} + 4 \cdot \frac{x^{\frac{3}{5}+1}}{\frac{3}{5}+1} + 3 \cdot \frac{x^{-4+1}}{-4+1} + x + C = \frac{6 \cdot x^{8}}{8} + \frac{4 \cdot x^{\frac{8}{5}}}{\frac{8}{5}} + \frac{3 \cdot x^{-3}}{-3}+x+C= \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-f59cd31b6d9358771df2a294cc601043_l3.png)





