Примеры решения определенных интегралов
Определенный интеграл от функции ![]() на промежутке
на промежутке ![]() обозначается
обозначается ![]() и равен разности двух значений первообразной функции, вычисленных при
и равен разности двух значений первообразной функции, вычисленных при ![]() и
и ![]() (формула Ньютона-Лейбница):
(формула Ньютона-Лейбница):
![]()
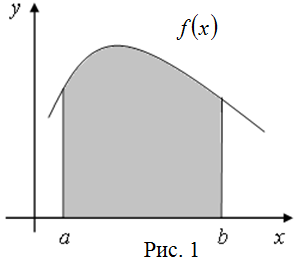
Геометрический смысл определенного интеграла. Определенный интеграл ![]() есть площадь криволинейной трапеции ограниченной графиком функции
есть площадь криволинейной трапеции ограниченной графиком функции ![]() , осью
, осью ![]() и прямыми
и прямыми ![]() и
и ![]() (рис. 1), то есть
(рис. 1), то есть
![]()
Для вычисления определенных интегралов подходят все методы, которые используются для нахождения неопределенных интегралов.
Примеры
| Задание | Вычислить интеграл
|
| Решение | Преобразуем подынтегральное выражение
Разобьем интеграл от суммы на сумму интегралов и вынесем за знак интеграла константы: Полученные интегралы являются табличными, вычислим их: |
| Ответ | 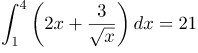 |
| Задание | Вычислить интеграл
|
| Решение | Вынесем константу за знак интеграла и вычислим полученный табличный интеграл:
|
| Ответ | 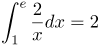 |
| Задание | Вычислить интеграл
|
| Решение | Сделаем замену |
| Ответ | 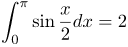 |
| Задание | Вычислить интеграл
|
| Решение | Внесем Подставляя все в исходный интеграл, получим: |
| Ответ | 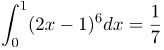 |
| Задание | Вычислить площадь криволинейной трапеции ограниченной функцией |
| Решение | Сделаем рисунок (рис. 2).
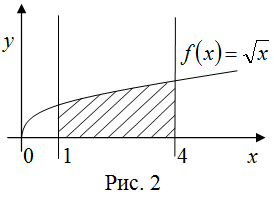
По геометрическому смыслу определенного интеграла нахождение площади заданной криволинейной трапеции сводится к вычислению интеграла Вычислим этот интеграл:
|
| Ответ | 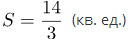 |






![Rendered by QuickLaTeX.com \[ \int _{1}^{4} \left( 2x+\frac{3}{\sqrt{x}} \right) dx = 2 \int _{1}^{4} x dx + 3 \int _{1}^{4} x^{-\frac{1}{2}} dx = 2 \cdot \frac{x^{1+1}}{1+1} \bigg| _{1}^{4} + 3 \cdot \frac{x^{-\frac{1}{2}+1}}{-\frac{1}{2}+1} \bigg| _{1}^{4} = \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-b4a25e85ad499ec899aea2dd92c2ef1a_l3.png)
![Rendered by QuickLaTeX.com \[ = 2 \cdot \frac{x^{2}}{2} \bigg| _{1}^{4} + 3 \cdot \frac{x^{\frac{1}{2}}}{\frac{1}{2}} \bigg| _{1}^{4} = x^{2} \bigg| _{1}^{4} + 6 \sqrt{x} \bigg| _{1}^{4} = (4^{2}-1^{2}) + 6 (\sqrt{4}-\sqrt{1}) = \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-bb282f9ec12d2ef8ba9c3f388c69a167_l3.png)
![Rendered by QuickLaTeX.com \[ \int _{0}^{\pi} \sin \frac{x}{2} dx = \int _{0}^{\frac{\pi}{2}} \sin t \cdot 2 dt = 2 \int _{0}^{\frac{\pi}{2}} \sin t dt = 2 (- \cos t) \bigg| _{0}^{\frac{\pi}{2}} = 2 \left( -\cos \frac{\pi}{2} - (-\cos 0) \right) = \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-2d249335175d2cb2fe30572c7ae446e8_l3.png)
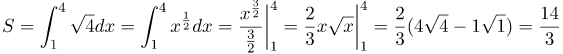 (кв. ед.)
(кв. ед.)




