Примеры решения интегралов
Теория про интегралы
Функция ![]() называется первообразной функции
называется первообразной функции ![]() , если
, если ![]() . Таким образом, интегрирование является операцией обратной к дифференцированию.
. Таким образом, интегрирование является операцией обратной к дифференцированию.
![]()
Для нахождения определенных и неопределенных интегралов используют свойства этих интегралов, таблицу интегралов, а также два основных метода интегрирования: замену переменных и интегрирование по частям.
Примеры
| Задание | Найти неопределенный интеграл
|
| Решение | Запишем подынтегральное выражение в следующем виде, используя свойства степеней:
Далее воспользуемся формулой для нахождения интеграла от степенной функции (ссылку на таблицу интегралов), получим: |
| Ответ | 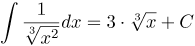 |
| Задание | Найти неопределенный интеграл
|
| Решение | Заменим интеграл суммы суммой интегралов:
Вынесем коэффициенты за знак интегралов: Полученные интегралы являются табличными, тогда окончательно получаем: |
| Ответ | 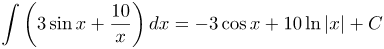 |
| Задание | Найти неопределенный интеграл
|
| Решение | Используя формулу понижения степени для подынтегральной функции:
Тогда Далее, согласно свойствам интегралов, вынесем коэффициент за знак интеграла и заменим интеграл от суммы на сумму интегралов: Находя полученные табличные интегралы, окончательно получим: |
| Ответ |  |
| Задание | Найти неопределенный интеграл
|
| Решение | Ведем замену
Подставляя введенную замену в интеграл и затем вынесем коэффициент за знак интеграла: Используя таблицу интегралов, окончательно будем иметь: Сделаем обратную замену, подставляем |
| Ответ | 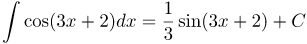 |
| Задание | Вычислить определенный интеграл
|
| Решение | Разобьем заданный интеграл разности на разность двух интегралов и вынесем во втором интеграле коэффициент за знак интеграла, получим:
Используя формулу для нахождения интеграла от степенной функции Далее, подставляем верхние и нижние пределы интегрирования (используем формулу Ньютона-Лейбница): |
| Ответ | 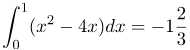 |






![Rendered by QuickLaTeX.com \[ \int \frac{1}{\sqrt[3]{x^{2}}} dx = \int x^{-\frac{2}{3}} dx = \frac{x^{-\frac{2}{3} + 1}}{-\frac{2}{3}+1} + C = \frac{x^{\frac{1}{3}}}{\frac{1}{3}} + C = 3 \cdot \sqrt[3]{x} + C \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-3519b6e7d97f31496f9da494ef58df98_l3.png)





