Универсальная тригонометрическая подстановка
Остальные тригонометрические функции выражаются через тангенс половинного аргумента следующим образом:
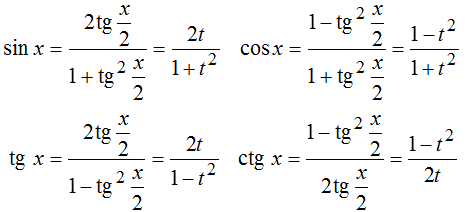
Данные формулы имеют смысл, когда определен ![]() , то есть при
, то есть при ![]() . И для двух последних формул
. И для двух последних формул
![]()
![]()
Указанная универсальная тригонометрическая подстановка позволяет свести интеграл от некоторой рациональной функции от ![]() и
и ![]() –
– ![]() к интегралу от рациональной дроби.
к интегралу от рациональной дроби.
Если ![]() , тогда
, тогда
![]()
Дифференцируя левую и правую части последнего равенства, будем иметь выражения для дифференциала переменной интегрирования:
![]()
Примеры решения задач
| Задание | Найти интеграл
|
| Решение | Подынтегральная функция |
| Ответ | 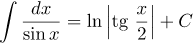 |
| Задание | Решить интеграл
|
| Решение | Подынтегральная функция является рациональной функцией от синуса и косинуса, поэтому для нахождения заданного интеграла можно применить универсальную тригонометрическую подстановку |
| Ответ | 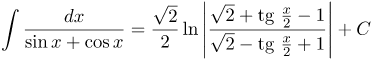 |






![Rendered by QuickLaTeX.com \[\int{\frac{dx}{\sin x}}\ \left\| \begin{matrix} \text{tg}\ \frac{x}{2}=t \\ \sin x=\frac{2t}{1+{{t}^{2}}} \\ dx=\frac{2dt}{1+{{t}^{2}}} \\ \end{matrix} \right\|=\int{\frac{\frac{2dt}{1+{{t}^{2}}}}{\frac{2t}{1+{{t}^{2}}}}}=\int{\frac{dt}{t}}=\ln \left| t \right|+C=\ln \left| \text{tg}\ \frac{x}{2} \right|+C\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-acffc045cc1d6a2b2f094149737187e6_l3.png)
![Rendered by QuickLaTeX.com \[\int{\frac{dx}{\sin x+\cos x}}\ \left\| \begin{matrix} \text{tg}\ \frac{x}{2}=t \\ \sin x=\frac{2t}{1+{{t}^{2}}} \\ \cos x=\frac{1-{{t}^{2}}}{1+{{t}^{2}}} \\ dx=\frac{2dt}{1+{{t}^{2}}} \\ \end{matrix} \right\|=\int{\frac{\frac{2dt}{1+{{t}^{2}}}}{\frac{2t}{1+{{t}^{2}}}+\frac{1-{{t}^{2}}}{1+{{t}^{2}}}}}=2\int{\frac{dt}{2t+1-{{t}^{2}}}}=\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-87ad2285147c6c9dd5892f581a74d34b_l3.png)
![Rendered by QuickLaTeX.com \[=2\int{\frac{dt}{2-{{\left( t-1 \right)}^{2}}}}=2\cdot \frac{1}{2\sqrt{2}}\ln \left| \frac{\sqrt{2}+\left( t-1 \right)}{\sqrt{2}-\left( t-1 \right)} \right|+C=\frac{\sqrt{2}}{2}\ln \left| \frac{\sqrt{2}+\text{tg}\ \frac{x}{2}-1}{\sqrt{2}-\text{tg}\ \frac{x}{2}+1} \right|+C\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-d91b4d88a9d584473162f5261ce3b295_l3.png)





