Геометрический и физический смысл определенного интеграла
Геометрический смысл определенного интеграла
Если функция ![]() непрерывна и положительна на некотором отрезке
непрерывна и положительна на некотором отрезке ![]() , то интеграл
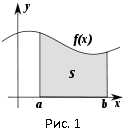
, то интеграл ![]() равен площади криволинейной трапеции, которая ограничена осью абсцисс, графиком функции
равен площади криволинейной трапеции, которая ограничена осью абсцисс, графиком функции ![]() и вертикальными прямыми
и вертикальными прямыми ![]() и
и ![]() (рис. 1):
(рис. 1):
![Rendered by QuickLaTeX.com \[S=\int\limits_{a}^{b}{f\left( x \right)dx}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-6e6a937e661c176ba6d2a4550375cfc8_l3.png)
| Задание | Найти площадь криволинейной трапеции, ограниченной графиком функции |
| Решение | Согласно геометрическому смыслу определенного интеграла, имеем, что искомая площадь равна
Помните, что мы искали площадь криволинейной трапеции, поэтому ответ выражается в квадратных единицах. |
| Ответ | 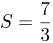 |
Физический смысл определенного интеграла
Пусть некоторая материальная точка ![]() перемещается под действием силы
перемещается под действием силы ![]() , которая направлена вдоль оси абсцисс (здесь
, которая направлена вдоль оси абсцисс (здесь ![]() – абсцисса движущейся точки
– абсцисса движущейся точки ![]() ).
).
Работа переменной силы ![]() , величина которой есть непрерывная функция
, величина которой есть непрерывная функция ![]() , действующей на отрезке
, действующей на отрезке ![]() , равна определенному интегралу от величины
, равна определенному интегралу от величины ![]() силы, взятому по этому отрезку:
силы, взятому по этому отрезку:
![Rendered by QuickLaTeX.com \[A=\int\limits_{a}^{b}{F\left( x \right)dx}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-6cf1dfde495eda9b6268dda4aa8502e4_l3.png)
| Задание | Найти работу материальной точки, которая перемещается под действием силы |
| Решение | По физическому смыслу определенного интеграла, искомая работа равна
|
| Ответ |






![Rendered by QuickLaTeX.com \[S=\int\limits_{1}^{2}{{{x}^{2}}dx}=\left. \frac{{{x}^{3}}}{3} \right|_{1}^{2}=\frac{1}{3}\cdot \left( {{2}^{3}}-{{1}^{3}} \right)=\frac{1}{3}\cdot 7=\frac{7}{3}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-68931fd6a66a2e491b3f4c42d6f0d9e2_l3.png)
![Rendered by QuickLaTeX.com \[A=\int\limits_{2}^{4}{\left( x-2 \right)dx}=\left. \left( \frac{{{x}^{2}}}{2}-2x \right) \right|_{2}^{4}=\frac{{{4}^{2}}}{2}-2\cdot 4-\left( \frac{{{2}^{2}}}{2}-2\cdot 2 \right)=2\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-8e3083ccfe8912b7d5211a61aafd15d9_l3.png)





