Решение интегралов методом подстановки

Рассмотрим неопределенный интеграл $\int{f\left( x \right)dx}$ некоторой функции $f\left( x \right)$ . Для упрощения вычисления интеграла часто удобно выполнить замену переменной. Переход от переменной интегрирования $x$ к новой переменной $t$ заменой (подстановкой) $x=\phi \left( t \right)$ называется методом подстановки (заменой переменной) в неопределенном интеграле.

Этот процесс описывается следующим образом:

$\int{f\left( x \right)dx}=\int{f\left( \phi \left( t \right) \right)\cdot {\phi }'\left( t \right)dt}=F\left( t \right)+C=F\left( {{\phi }^{-1}}\left( x \right) \right)+C$

Здесь обратная функция $t={{\phi }^{-1}}\left( x \right)$ описывает зависимость новой переменной $t$ от старой переменной $x$ .

ЗАМЕЧАНИЕ

Дифференциал $dx$ должен быть обязательно заменен на дифференциал новой переменной $dt$ .

Примеры решения задач

ПРИМЕР 1

Задание	Найти интеграл $\int{{{\sin }^{3}}x\cos xdx}$
Решение	Заменяем синус новой переменной, тогда $\int{{{\sin }^{3}}x\cos xdx}\ \left\\| \begin{matrix} \sin x=t \\ \cos xdx=dt \\ \end{matrix} \right\\|=\int{{{t}^{3}}dt}=\frac{{{t}^{4}}}{4}+C=\frac{{{\sin }^{4}}x}{4}+C$
Ответ

ПРИМЕР 2

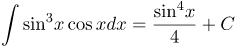Задание

Решить интеграл $\int{x{{\left( x+1 \right)}^{100}}dx}$

Решение

Делаем следующую замену:

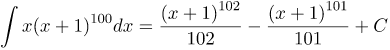$\int{x{{\left( x+1 \right)}^{100}}dx}\ \left\| \begin{matrix} x+1=t \\ x=t-1 \\ dx=dt \\ \end{matrix} \right\|=\int{\left( t-1 \right)\cdot {{t}^{100}}dt}=\int{\left( {{t}^{101}}-{{t}^{100}} \right)dt}=$

$=\int{{{t}^{101}}dt}-\int{{{t}^{100}}dt}=\frac{{{t}^{102}}}{102}-\frac{{{t}^{101}}}{101}+C=\frac{{{\left( x+1 \right)}^{102}}}{102}-\frac{{{\left( x+1 \right)}^{101}}}{101}+C$

Ответ

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Решение интегралов методом подстановки

Примеры решения задач