Геометрический смысл дифференциала функции
Рассмотрим функцию ![]() Проведем к графику этой функции касательную
Проведем к графику этой функции касательную ![]() в точке
в точке ![]() и рассмотрим ординату этой касательной для точки
и рассмотрим ординату этой касательной для точки ![]() (рис. 1). На рисунке
(рис. 1). На рисунке
![]()
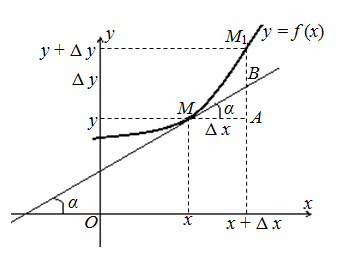
Рисунок 1
Рассмотрим прямоугольный ![]() Тогда
Тогда
![]()
Согласно геометрическому смыслу производной, тангенс угла между касательной к графику функции ![]() и положительным направлением оси абсцисс равен производной этой функции:
и положительным направлением оси абсцисс равен производной этой функции:
![]()
Следовательно,
![]()
Известно, что приращение независимой переменной равно дифференциалу этой переменной:
![]()
Тогда
![]()
По определению, дифференциал ![]() функции
функции ![]() равен
равен
![]()
Сравнивая правые части последних двух равенств, делаем вывод, что равны и их левые части, то есть
![]()











