Таблица производных

ПРИМЕР 1

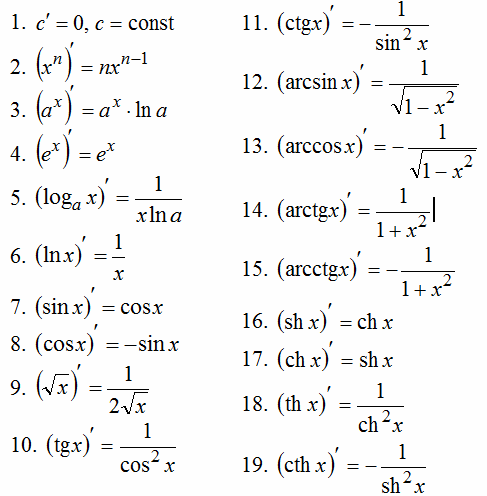
Задание

Найти производную функции $y = x^2 + 4$

Решение

Искомая производная

$y' = \left( x^2 + 4 \right)'$

Согласно правилам дифференцирования (нахождения производной), производная суммы равна сумме производных, то есть

$y' = \left( x^2 \right)' + \left( 4 \right)'$

Производную первого слагаемого находим как производную степенной функции (формула № 2 в таблице производных), а второго – как производную константы (формула № 1 в таблице):

$y' = 2x^{2-1} + 0 = 2x$

Ответ

$y' = 2x$

ПРИМЕР 2

Задание

Найти производную функции $y = \cos x - \ln x$

Решение

Продифференцируем заданную функцию:

$y' = (\cos x - \ln x)'$

Производная разности равна разности производных:

$y' = (\cos x)' - (\ln x)'$

Производная косинуса равна минус синусу (формула № 8 в таблице производных), а производную натурального логарифма находим по формуле № 6 из таблицы. Получаем:

$y' = - \sin x - \frac{1}{x}$

Ответ

$y' = - \sin x - \frac{1}{x}$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Таблица производных