Правила дифференцирования
К основным правилам дифференцирования относят:
1. Вынесение постоянного множителя за знак производной:
![]()
То есть константу можно выносить за знак производной.
| Задание | Найти производную функции |
| Решение | Продифференцируем заданную функцию:
Согласно правилу вынесения константы за знак производной, последнее равенство можно записать в виде: По таблице производных находим, что Тогда получаем: |
| Ответ |
2. Производная суммы, производная разности:
![]()
Производная суммы двух функций равна сумме производных от каждой из них.
Замечание. Это правило распространяется и на большее число функций.
![]()
равна разности производных от каждой из них.
| Задание | Найти производную функции |
| Решение | Искомая производная
Согласно правилу, производная суммы/разности функций равна сумме/разности производных от каждой из них: |
| Ответ |
3. Производная произведения:
![]()
Производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
| Задание | Найти производную функции |
| Решение | Искомая производная
Согласно правилу дифференцирования произведения, имеем: |
| Ответ | 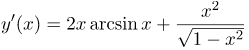 |
4. Производная дроби (производная частного двух функций):
![Rendered by QuickLaTeX.com \[ \left( \frac{f(x)}{g(x)} \right)' = \frac{(f(x))' \cdot g(x) - f(x) \cdot (g(x))'}{(g(x))^2} \text{ },\text{ } g(x) \ne 0 \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-2433269b96ed239cb232eef01c8f810d_l3.png)
Итак, производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя.
| Задание | Найти производную функции
|
| Решение | Искомая производная равна:
Исходная функция представляет собой отношение двух функций: Применяя таблицу производных и правило дифференцирования суммы двух функций, получаем: Константу выносим за знак производной: |
| Ответ | 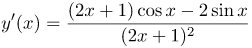 |











