Производная произведения

ОПРЕДЕЛЕНИЕ

Производная произведения равна производной первого сомножителя умноженной на второй плюс первый сомножитель умноженный на производную второго.

$\left( u \cdot v \right)' = \left( u \right)' \cdot v + u \cdot \left( v \right)'$

Стоит запомнить, что производная произведения НЕ РАВНА произведению производных.

Примеры решения задач по теме «Производная произведения»

ПРИМЕР 1

Задание

Решение

Искомая производная

$y'(x) = \left( (x+1) \ln x\right)'$

Таким образом, надо найти производную произведения двух функций $u(x)=x+1$ и $v(x) = \ln x$ . Тогда по формуле имеем:

$y'(x) = \left( (x+1) \ln x\right)' = \left( x+1 \right)' \cdot \ln x + (x+1) \cdot \left( \ln x\right)'$

Найдем производную функции $u(x)=x+1$ , то есть $\left( x+1 \right)'$ . Так как производная суммы равна сумме производных, то получаем:

$\left( x+1 \right)' = \left( x \right)' + \left( 1 \right)'$

Производная независимой переменной $x$ равна единице:

$\left( x \right)' = 1$

а производная единицы, как константы, равна нулю:

$\left( 1 \right)' = 0$

То есть

$\left( x+1 \right)' = \left( x \right)' + \left( 1 \right)' = 1+0=1$

Производная от натурального логарифма равна единице деленной на подлогарифмическую функцию:

$v'(x) = \left( \ln x \right)' = \frac{1}{x}$

Итак,

$y'(x) = \left( x+1 \right)' \cdot \ln x + (x+1) \cdot \left( \ln x\right)' = 1 \cdot \ln x + (x+1) \cdot \frac{1}{x} = \ln x + \frac{x+1}{x}$

Ответ

ПРИМЕР 2

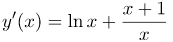Задание

Найти производную функции $y(x) = x e^{x}$

Решение

Искомая производная равна:

$y'(x) = \left( x e^{x} \right)'$

Применяем формулу «производная произведения» $\left( u \cdot v \right)' = \left( u \right)' \cdot v + u \cdot \left( v \right)'$ . Получаем:

$y'(x) = \left( x e^{x} \right)' = \left( x \right)' \cdot e^{x} + x \cdot \left( e^{x} \right)'$

$\left( x \right)' = 1$

$\left( e^{x} \right)' = e^{x}$

Таким образом,

$y'(x) = \left( x \right)' \cdot e^{x} + x \cdot \left( e^{x} \right)' = 1 \cdot e^{x} + x \cdot e^{x} = (x+1)e^{x}$

Ответ

$y'(x) = (x+1)e^{x}$

Понравился сайт? Расскажи друзьям!