Формулы дифференцирования функций

ОПРЕДЕЛЕНИЕ

Процесс нахождения производной называется дифференцированием. То есть дифференцирование – вычисление производных и дифференциалов любого порядка от функции одного переменного и частных производных и дифференциалов, а также полных дифференциалов от функций многих переменных.

Далее разобраны основные правила и формулы дифференцирования функций:

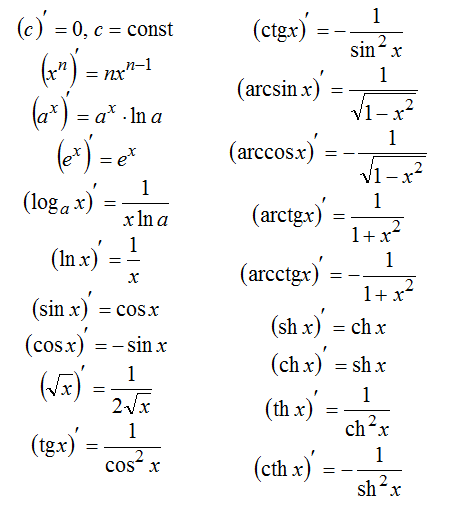
Правила дифференцирования:

Константу можно выносить за знак производной:

${{\left( c\cdot u\left( x \right) \right)}^{\prime }}=c\cdot {u}'\left( x \right)$

Производная суммы равна сумме производных:

${{\left( u\left( x \right)\pm v\left( x \right) \right)}^{\prime }}={u}'\left( x \right)\pm {v}'\left( x \right)$

Производная произведения равна сумме произведений производной первого слагаемого на второе и первого слагаемого на производную второго:

${{\left( u\left( x \right)\cdot v\left( x \right) \right)}^{\prime }}={u}'\left( x \right)v\left( x \right)+u\left( x \right){v}'\left( x \right)$

Производная частного находится по формуле:

${{\left( \frac{u\left( x \right)}{v\left( x \right)} \right)}^{\prime }}=\frac{{u}'\left( x \right)v\left( x \right)-u\left( x \right){v}'\left( x \right)}{{{v}^{2}}\left( x \right)},\ v\left( x \right)\ne 0$

ПРИМЕР 1

Задание

Найти производную функции

$y\left( x \right)=\frac{\sin x}{x}+2\sqrt{x+1}+2$

Решение

Используя правила дифференцирования и таблицу производных, имеем:

${y}'\left( x \right)={{\left( \frac{\sin x}{x}+2\sqrt{x+1}+2 \right)}^{\prime }}={{\left( \frac{\sin x}{x} \right)}^{\prime }}+{{\left( 2\sqrt{x+1} \right)}^{\prime }}+{{\left( 2 \right)}^{\prime }}=$

$=\frac{{{\left( \sin x \right)}^{\prime }}\cdot x-\sin x\cdot {{\left( x \right)}^{\prime }}}{{{\left( x \right)}^{2}}}+2\cdot {{\left( \sqrt{x+1} \right)}^{\prime }}+0=\frac{\cos x\cdot x-\sin x\cdot 1}{{{x}^{2}}}+2\cdot \frac{1}{2\sqrt{x+1}}\cdot {{\left( x+1 \right)}^{\prime }}=$

$=\frac{x\cos x-\sin x}{{{x}^{2}}}+\frac{1}{\sqrt{x+1}}\cdot {{\left( 1+0 \right)}^{\prime }}=\frac{x\cos x-\sin x}{{{x}^{2}}}+\frac{1}{\sqrt{x+1}}$

Ответ

ПРИМЕР 2

Задание

Найти производную функции $y=6-2x+{{x}^{4}}-\cos x+3\sqrt{x}$

Решение

Продифференцируем заданное выражение:

${y}'={{\left( 6-2x+{{x}^{4}}-\cos x+3\sqrt{x} \right)}^{\prime }}$

Производная суммы/разности равна сумме/разности производных, таким образом, можем записать:

${y}'={{\left( 6 \right)}^{\prime }}-{{\left( 2x \right)}^{\prime }}+{{\left( {{x}^{4}} \right)}^{\prime }}-{{\left( \cos x \right)}^{\prime }}+{{\left( 3\sqrt{x} \right)}^{\prime }}$

Используя свойства дифференцирования и таблицу производных, получаем:

${y}'=0-2\cdot 1+4{{x}^{4-1}}-\left( -\sin x \right)+3\cdot \frac{1}{2\sqrt{x}}=-2+4{{x}^{3}}+\sin x+\frac{3}{2\sqrt{x}}$

Ответ

${y}'=-2+4{{x}^{3}}+\sin x+\frac{3}{2\sqrt{x}}$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Формулы дифференцирования функций

Правила дифференцирования: