Полный дифференциал функции

ОПРЕДЕЛЕНИЕ

Полным приращением функции $u = f(x, y, z)$ называется разность $\Delta u = f(x + \Delta x, y + \Delta y, z + \Delta z) - f(x, y, z) .$

ОПРЕДЕЛЕНИЕ

Главная часть полного приращения функции $u = f(x, y, z) ,$ которая линейно зависит от приращений независимых переменных $\Delta x, \Delta y$ и $\Delta z ,$ называется полным дифференциалом функции $u = f(x,y,z)$ и обозначается $du .$

Если функция имеет непрерывные частные производные, то полный дифференциал определяется формулой:

$du = d_xu + d_yu + d_zu$

или, что то же самое:

$du = u'_xd_x + u'_yd_y + u'_zd_z$

где $d_xu, d_yu, d_zu$ – частные дифференциалы заданной функции по соответствующей переменной.

ПРИМЕР

Задание

Найти полный дифференциал функции

$z = \ln \left( x + \sqrt{x^2 + y^2} \right) -3$

Решение

Находим частные производные функции по каждой из переменных:

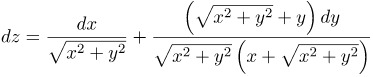$\frac{\partial z}{\partial x} = \frac{1}{x + \sqrt{x^2 + y^2}} \cdot \left( 1 + \frac{1}{2 \sqrt{x^2 + y^2}} \cdot 2x \right) - 0 =$

$= \frac{1}{x + \sqrt{x^2 + y^2}} \cdot \frac{\sqrt{x^2 + y^2} + x}{\sqrt{x^2 + y^2}} = \frac{1}{\sqrt{x^2 + y^2}}$

$\frac{\partial z}{\partial y} = \frac{1}{x + \sqrt{x^2 + y^2}} \cdot \left( 1 + \frac{1}{2 \sqrt{x^2 + y^2}} \cdot 2y \right) - 0 =$

$= \frac{1}{x + \sqrt{x^2 + y^2}} \cdot \frac{\sqrt{x^2 + y^2} + y}{\sqrt{x^2 + y^2}} = \frac{\sqrt{x^2 + y^2} + y}{\sqrt{x^2 + y^2} \left( x + \sqrt{x^2 + y^2}\right)}$

Тогда искомый дифференциал

$dz = \frac{1}{\sqrt{x^2 + y^2}}dx + \frac{\sqrt{x^2 + y^2} + y}{\sqrt{x^2 + y^2} \left( x + \sqrt{x^2 + y^2}\right)}dy =$

$= \frac{dx}{\sqrt{x^2 + y^2}} + \frac{\left( \sqrt{x^2 + y^2} + y \right) dy}{\sqrt{x^2 + y^2} \left( x + \sqrt{x^2 + y^2}\right)}$

Ответ

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Полный дифференциал функции