Дифференциал параметрической функции
ОПРЕДЕЛЕНИЕ
Если функция 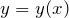 задана в виде
задана в виде 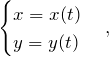 где
где 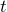 – параметр, то говорят, что эта функция задана параметрически.
– параметр, то говорят, что эта функция задана параметрически.
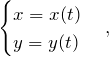 где
где Чтобы найти дифференциал ![]() этой функции, необходимо вначале найти ее производную
этой функции, необходимо вначале найти ее производную
![]()
,а затем подставить полученное выражение в формулу для дифференциала ![]()
ПРИМЕР
| Задание | Найти дифференциал функции |
| Решение | Находим производную заданной функции Тогда Отсюда, дифференциал |
| Ответ |






![Rendered by QuickLaTeX.com \[ \begin{cases} x(t) = t^2\\ y(t) = t^3 \end{cases} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-5de8bd821199d01755e1387775f4f982_l3.png)





