Дифференциал неявной функции
По определению дифференциал функции ![]() равен
равен
![]()
То есть вначале надо найти производную заданной неявно функции ![]() а затем подставить ее в последнее соотношение.
а затем подставить ее в последнее соотношение.
Чтобы найти указанную производную, необходимо продифференцировать обе части уравнения ![]() и из полученного равенства выразить производную
и из полученного равенства выразить производную ![]()
Отметим, что при дифференцировании надо не забывать, что ![]() не является независимой переменной, а есть функция от
не является независимой переменной, а есть функция от ![]() поэтому производную от нее надо находить как от сложной функции.
поэтому производную от нее надо находить как от сложной функции.
Примеры вычисления дифференциалов неявных функций
| Задание | Найти дифференциал |
| Решение | Дифференцируем левую и правую части заданного равенства:
Согласно свойствам производной, производная суммы равна сумме производных. Тогда имеем: Применяем правило дифференцирования произведения: Из последнего равенства находим производную Итак, искомый дифференциал |
| Ответ | 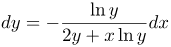 |
| Задание | Найти дифференциал функции |
| Решение | Вначале по свойствам логарифмов упростим выражение. Известно, что логарифм произведения равен сумме логарифмов от каждого из сомножителей, то есть имеем:
Дифференцируем левую и правую части последнего равенства: Производная суммы равна сумме производных, а также производная константы равна нулю. Тогда получаем: Находим записанные производные и производную от А тогда искомый дифференциал |
| Ответ | 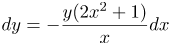 |











