Дифференциал второго порядка
Дифференциалом второго порядка или вторым дифференциалом называется дифференциал первого порядка от дифференциала первого порядка заданной функции и обозначается через ![]()
![]()
Для вычисления дифференциала второго порядка применяется формула:
![]()
| Задание | Найти дифференциал второго функции |
| Решение | По определению второй дифференциал равен
Найдем вторую производную заданной функции. Для этого вначале продифференцируем ее по переменной Вторая производная заданной функции: Тогда искомый дифференциал второго порядка заданной функции |
| Ответ | 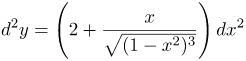 |
| Задание | Найти дифференциал второго порядка |
| Решение | Найдем первый дифференциал Согласно свойствам дифференциалов, дифференциал суммы равен суме дифференциалов, а дифференциал константы – нулю: По свойствам расписываем дифференциал произведения: Далее находим второй дифференциал Расписываем дифференциал частного по соответствующему свойству: |
| Ответ | 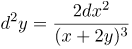 |






![Rendered by QuickLaTeX.com \[ d^2y = \left( 2 - \frac{x}{\sqrt{(1 - x^2)^3}} \right) dx^2 \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-4967ac8a00886a6945829dc1541881e7_l3.png)
![Rendered by QuickLaTeX.com \[ = \frac{-dy \cdot (x + 2y) + y \cdot [d(x) + d(2y)]}{(x + 2y)^2}dx = \frac{-\frac{-ydx}{x + 2y} \cdot (x + 2y) + y \cdot (dx + 2dy)}{(x + 2y)^2}dx = \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-9212e40503a6dc5d8362de4ec331e7d3_l3.png)
![Rendered by QuickLaTeX.com \[ = \frac{ydx + ydx + 2ydy}{(x + 2y)^2}dx = \frac{2ydx + 2y \cdot \frac{-ydx}{x + 2y}}{(x + 2y)^2}dx = \frac{2y(x + 2y) - 2y^2}{(x + 2y)^3}(dx)^2 = \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-c5cdaca5e90e587d765a37eeeb241cc7_l3.png)
![Rendered by QuickLaTeX.com \[ = \frac{2 \left(\overbrace{xy + y^2}^{=1} \right)}{(x + 2y)^3}dx^2 = \frac{2dx^2}{(x + 2y)^3} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-53e308e74c16783dacacd6b3e8781b9a_l3.png)





