Свойства производных

Пусть функции $u = u(x)$ и $v = v(x)$ являются дифференцируемыми, $c_1$ и $c_2$ – произвольные константы. Тогда имеют место следующие соотношения:

1. Линейность:

$(c_1u \pm c_2v)' = c_1 \cdot u' \pm c_2 \cdot v'$

ПРИМЕР

$(2x^2 - 3 \sin x)' = 2 \cdot (x^2)' - 3 \cdot (\sin x)'$

2. Производная произведения:

$(u \cdot v)' = u' \cdot v + u \cdot v'$

ПРИМЕР

$(\sin x \cdot \arcsin x)' = (\sin x)' \cdot \arcsin x + \sin x \cdot (\arcsin x)'$

3. Производная частного:

$\left( \frac{u}{v} \right)' = \frac{u'v - uv'}{v^2} \text{ },\text{ } v \ne 0$

ПРИМЕР

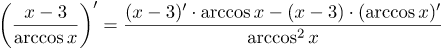
4. Постоянный множитель можно выносить за знак производной:

$(c \cdot u)' = c \cdot u'$

ПРИМЕР

$(2 \text{ tg }x)' = 2 \cdot (\text{tg }x)'$

5. Производная сложной функции: если задана функция $y = f(u)$ , у которой аргумент есть в свою очередь функцией от $x: u = g(x) ,$ то производная $y'(x)$ равна:

$y'(x) = y'(u) \cdot u'(x)$

ПРИМЕР

$\left( \overbrace{\cos \underbrace{(2x - 3)}_{u(x)}}^{y(u)} \right)' \bigg| \bigg|(\cos x)' = -\sin x \bigg| \bigg| = -\sin (2x - 3) \cdot (2x - 3)'$

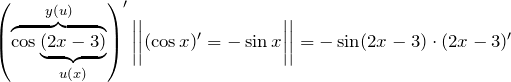6. Производная обратной функции: если функция $x(y)$ , является обратной к функции $y(x) ,$ то их производные связаны соотношением:

$y'(x) = \frac{1}{x'(y)}$

ПРИМЕР

Рассмотрим функцию $y = \arcsin x$ , обратной к ней есть функция $x(y) = \sin y .$ Найдем производные:

$y'(x) = (\arcsin x)' = \frac{1}{\sqrt{1 - x^2}}$

$\frac{1}{x'(y)} = \frac{1}{(\sin y)'} = \frac{1}{\cos y} = \frac{1}{\sqrt{1 - \sin^2 y}} ||y = \arcsin x|| = \frac{1}{\sqrt{1 - \sin^2(\arcsin x)}} = \frac{1}{\sqrt{1 - x^2}}$

то есть

$y'(x) = \frac{1}{x'(y)}$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Свойства производных