Формулы производных функции
Рассмотрим функцию ![]() которая определена и непрерывна на некотором интервале
которая определена и непрерывна на некотором интервале ![]() произвольную точку
произвольную точку ![]() и соответствующее значение функции в этой точке
и соответствующее значение функции в этой точке ![]() Зададим аргументу функции приращение
Зададим аргументу функции приращение ![]() в точке
в точке ![]() В результате получим величину
В результате получим величину ![]() и соответствующее значение функции
и соответствующее значение функции ![]()
![]()
Если данный предел конечен, то рассматриваемая функция ![]() называется дифференцируемой в точке
называется дифференцируемой в точке ![]() .
.
Дифференцирование – это процесс нахождения производной функции. Его проводят с использованием таблицы производных и правил дифференцирования. На этой странице разобраны все формулы производных функции.
Таблица производных, список формул
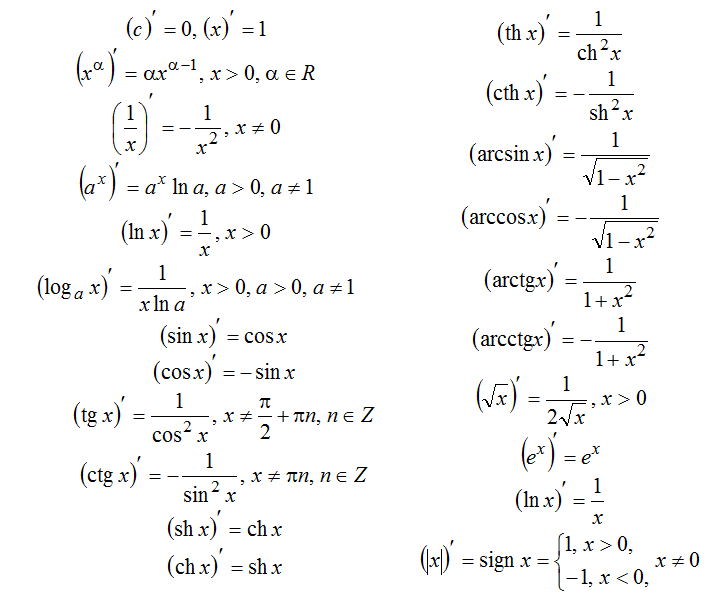
Правила дифференцирования
![]()
![]()
![]()
![]()
| Задание | Найти производную функции |
| Решение | Искомая производная равна:
|
| Ответ |
| Задание | Продифференцировать функцию
|
| Решение | Искомая производная
Производная разности равна разности производных: Производную первого слагаемого найдем по таблице производных, второго – как производную частного: |
| Ответ | 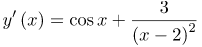 |











