Производная числа умноженного на икс
![]()
Эту формулу легко получить с помощью правила дифференцирования, которое гласит, что константу можно выносить за знак производной, и того факта, что производная независимой переменной ![]() равна единице:
равна единице:
![]()
Примеры решения задач
| Задание | Найти производную функции |
| Решение | Искомая производная равна:
Производная разности функций равна разности производных от каждой из функций: Производная от Производная от числа 17 (константы) равна нулю: Тогда, |
| Ответ |
| Задание | Найти производную функции |
| Решение | Искомая производная
Производная от корня равна единице деленной на два таких же корня: Производная от суммы двух функций равна сумме производных от каждого из слагаемых: Производная от слагаемого Производная от единицы, как от константы, равна нулю: Тогда |
| Ответ | 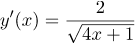 |











