Производная первого порядка
Производная первого порядка функции ![]() , заданной явно, находится с помощью таблицы производных
, заданной явно, находится с помощью таблицы производных
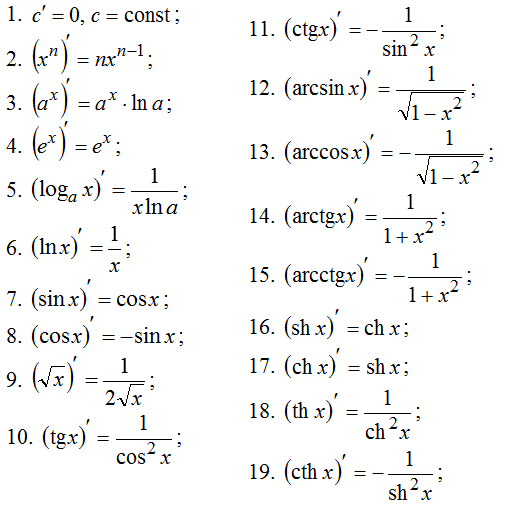
а также правил дифференцирования (нахождения производных):
- Константу можно выносить за знак производной:
![Rendered by QuickLaTeX.com \[ (c \cdot u(x))' = c \cdot (u(x))' ; \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-7e56db27dd5b34414f9feb3a3b7ade39_l3.png)
- Производная суммы/разности:
![Rendered by QuickLaTeX.com \[ (u \pm v)' = u' \pm v' \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-2a51b7570b4072b5b74bbe524fd79c4f_l3.png)
- Производная произведения:
![Rendered by QuickLaTeX.com \[ (u \cdot v)' = u' \cdot v + u \cdot v' \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-1356a9c11dc7765932ffe0082a9b51ca_l3.png)
- Производная частного двух функций:
![Rendered by QuickLaTeX.com \[ \left( \frac{u}{v} \right)' = \frac{u'v - uv'}{v^2} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-009c0eaee84d9f2d878310f868429fe0_l3.png)
| Задание | Найти производную функции, заданной явно
|
| Решение | Искомая производная
Производная суммы/разности функций равна сумме/разности их производных, то есть: Производную первого слагаемого находим по таблице производных как производную степенной функции Во втором слагаемом, согласно свойствам производных, вначале вынесем константу 3 за знак производной: А затем производную найдем по выше предложенной формуле производной степенной функции: Производную третьего слагаемого находим как производную частного по формуле А таким образом, для заданной функции имеем: |
| Ответ | 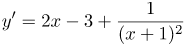 |
Производная первого порядка параметрической функции
В случае если функция ![]() задана параметрически в виде
задана параметрически в виде 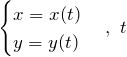 – параметр, то первая производная такой функции находится по формуле:
– параметр, то первая производная такой функции находится по формуле:
![]()
| Задание | Найти первую производную функции заданной параметрически
|
| Решение | Согласно формуле, нам необходимо найти производные каждой из функций по параметру Тогда искомая производная |
| Ответ |
Производная первого порядка неявной функции
Если функция ![]() задана неявно равнение
задана неявно равнение ![]() или
или ![]() то для нахождения первой производной
то для нахождения первой производной ![]() поступают следующим образом:
поступают следующим образом:
- дифференцируют левую и правую части заданного равенства:
![Rendered by QuickLaTeX.com \[ (F(x ; y(x)))' = (0)' \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-58242ced544659b6dba1167215aa0b10_l3.png)
или
![Rendered by QuickLaTeX.com \[ (F(x ; y(x)))' = (G(x ; y(x)))' ; \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-82fdd06aef019d8fcfd8af74482364ad_l3.png)
- находят производные от каждой из частей равенства, используя таблицу производных и правила дифференцирования, а также учитывают, что
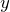 – сложная функция;
– сложная функция; - из полученного равенства выражают
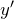 .
.
| Задание | Найти производную |
| Решение | Дифференцируем обе части заданного равенства:
Согласно правилам дифференцирования и таблице производных, имеем: Из полученного равенства находим |
| Ответ | 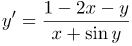 |






![Rendered by QuickLaTeX.com \[ \begin{cases} x = \ln t \\ y = t^2 - 1 \end{cases} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-59898f82df552adb710b3e5bfd37da2f_l3.png)





