Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Главная Справочник Производные Таблица производных сложных функций

Таблица производных сложных функций

ПРИМЕР 1

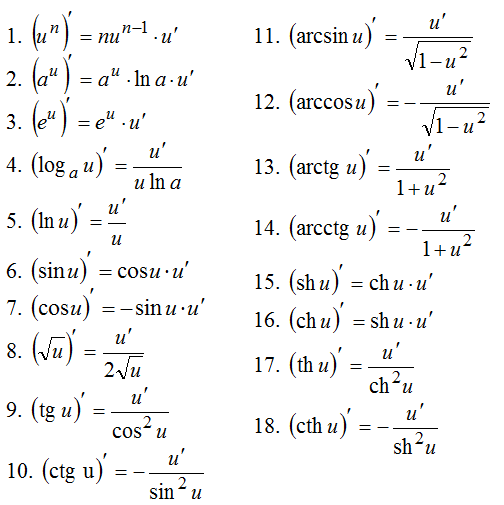
Задание

Найти производную функции $y(x) = \arcsin 2x - e^{2x - 3}$

Решение

Искомая производная равна:

$y'(x) = \left( \arcsin 2x - e^{2x - 3} \right)'$

Производная разности равна разности производных, то есть

$y'(x) = ( \arcsin 2x )' - \left( e^{2x - 3} \right)'$

Производную арксинуса найдем по формуле

$( \arcsin u )' = \frac{u'}{\sqrt{1-u^2}}$

а для экспоненты используем формулу

$\left( e^u \right)' = e^u \cdot u'$

Тогда будем иметь:

$y'(x) = \frac{(2x)'}{\sqrt{1 - (2x)^2}} - e^{2x-3} \cdot (2x - 3)' = \frac{2 \cdot (x)'}{\sqrt{1 - 4x^2}} - e^{2x - 3} \cdot \left[(2x)' - (3)' \right] =$

$= \frac{2 \cdot 1}{\sqrt{1 - 4x^2}} - e^{2x - 3} \cdot \left[ 2 \cdot (x)' - 0 \right] = \frac{2}{\sqrt{1 - 4x^2}} - e^{2x - 3} \cdot (2 \cdot 1 - 0) =$

$= \frac{2}{\sqrt{1 - 4x^2}} - 2e^{2x - 3}$

Ответ

ПРИМЕР 2

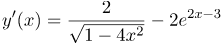Задание

Найти производную функции $y(x) = \sin (3x - 1)$

Решение

Продифференцируем функцию:

$y'(x) = \left( \sin (3x - 1) \right)'$

Производная синуса равна косинусу того же аргумента, умноженному на производную аргумента, то есть

$y'(x) = \cos (3x - 1) \cdot (3x - 1)' = \cos (3x - 1) \cdot \left[ (3x)' - (1)' \right] = \cos (3x - 1) \cdot \left[ 3 \cdot (x)' - 0 \right] =$

$= \cos (3x - 1) \cdot (3 \cdot 1 - 0) = 3 \cos (3x - 1)$

Ответ

$y'(x) = 3 \cos (3x - 1)$

© SolverBook - онлайн сервисы для учебы, 2015

Копирование материалов с сайта возможно только с разрешения
администрации портала и при наличие активной ссылки на источник.

Почта для связи: info@ru.solverbook.com

Выберите язык:

Сервисы

SolverBook