Примеры решения производных сложных функций
Пусть задана сложная функция ![]() , тогда производная этой сложной функции находится по правилу:
, тогда производная этой сложной функции находится по правилу:
![]()
иначе говоря, производная сложной функции берется по «правилу цепочки», то есть, сначала находится производная внешней функции, аргумент при этом не изменяется, а затем находится производная от её аргумента. Если же и он является сложной функцией, то процесс снова повторяется, пока не найдется производная от последнего независимого аргумента.
| Задание | Найти производную сложной функции |
| Решение | По правилу нахождения производной сложной функции вычислим сначала производною от корня и умножим её на производную подкоренного выражения
Производную подкоренного выражения находим, используя свойство линейности и таблицу производных: |
| Ответ | 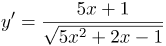 |
| Задание | Найти производную функции |
| Решение | По правилу дифференцирования сложной функции, сначала находим производную от экспоненты и умножаем её на производную её степени:
|
| Ответ |
| Задание | Найти производную функции сложной функции |
| Решение | По правилу нахождения производной сложной функции, производная этой функции равна произведению производной от функции арккотангенс на производную аргумента:
Аргумент является степенной функцией, поэтому производная от него равна |
| Ответ | 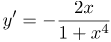 |
| Задание | Найти производную функции |
| Решение | Заданная функция является сложной, тогда по правилу вычисления производной сложной функции имеем:
|
| Ответ | 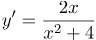 |
| Задание | Найти производную сложной функции |
| Решение | По правилу дифференцирования сложной функции возьмем сначала производную от заданной функции, как от степенной
Далее возьмем производную от полученной логарифмической функции Производная разности равна разности производных: Производная |
| Ответ | 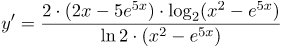 |











