Примеры решения производных
Теория про производные
Процесс отыскания производной называется дифференцированием.
На практике для нахождения производной чаще всего используют таблицу производных и основные правила вычисления производных:
- Линейность:
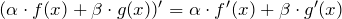
- Производная произведения:
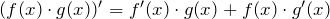
- Производная частного:
![Rendered by QuickLaTeX.com \[ \left( \frac{f(x)}{g(x)} \right)' = \frac{f'(x) \cdot g(x) - f(x) \cdot g'(x)}{g^{2}(x)} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-24897012a2f8808beadce0ee23f33e76_l3.png)
Примеры
| Задание | Найти производную функции |
| Решение | По свойству линейности производной, получим:
Далее воспользуемся таблицей производных элементарных функций: |
| Ответ |
| Задание | Найти производную функции |
| Решение | Производная суммы равна сумме производных и вынесем константу во втором слагаемом:
Далее используя таблицу производных, получим: |
| Ответ | 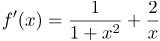 |
| Задание | Найти производную функции |
| Решение | Используя правило дифференцирования произведения, получим:
Далее воспользуемся таблицей производных для степенной и показательной функций, а также правилом дифференцирования разности: |
| Ответ |
| Задание | Найти производную функции
|
| Решение | По правилу дифференцирования частного имеем:
Применяя таблицу производных для степенной и логарифмической функций и преобразовывая полученное выражение, получим: |
| Ответ | 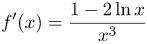 |
| Задание | Найти производную функции
|
| Решение | Представим заданную функцию в виде степени с отрицательным показателем, то есть Далее учитывая правило дифференцирования произведения двух функций, получим: Найдем необходимые производные, используя таблицу производных: Преобразовывая полученное выражение, окончательно получим |
| Ответ | 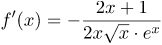 |






![Rendered by QuickLaTeX.com \[ f'(x) = \frac{(\ln x)' \cdot x^{2} - \ln x \cdot (x^{2})'}{\left( x^{2} \right)^{2}} = \frac{\frac{1}{x} \cdot x^{2} - \ln x \cdot 2x}{x^{4}} = \frac{x -2x \ln x}{x^{4}} = \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-e46a171ac9d170c808a144527c39d1ba_l3.png)
![Rendered by QuickLaTeX.com \[ f'(x) = -\left( \sqrt{x} \cdot e^{x} \right)^{-2} \cdot \left( \sqrt{x} \cdot e^{x} \right)' = -\frac{1}{\left( \sqrt{x} \cdot e^{x} \right)^{2}} \cdot \left( \sqrt{x} \cdot e^{x} \right)' = - \frac{\left( \sqrt{x} \right)' \cdot e^{x} + \sqrt{x} \cdot \left( e^{x} \right)'}{x \cdot e^{2x}} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-1f110f76439d2193c6be42fca6bbb98e_l3.png)
![Rendered by QuickLaTeX.com \[ f'(x) = -\frac{\frac{1}{2 \sqrt{x}} \cdot e^{x} + \sqrt{x} \cdot e^{x}}{x \cdot e^{2x}} = -\frac{e^{x}+ 2x \cdot e^{x}}{2x \sqrt{x} \cdot e^{2x}} =- \frac{e^{x}(2x+1)}{2x \sqrt{x} \cdot e^{2x}} = -\frac{2x+1}{2x \sqrt{x} \cdot e^{x}} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-80ab12537e4211fd72e9f4add8479d51_l3.png)





