Примеры решения частных производных

Теория по частным производным

Пусть функция двух переменных $z=f(x, y)$ – непрерывна и дифференцируема. Частной производной $\frac{\partial z}{\partial x}$ по $x$ называется производная от этой функции по $x$ при условии, что $y$ – константа. Частной производной $\frac{\partial z}{\partial y}$ по $y$ называется производная от этой функции по $y$ при условии, что $x$ – константа.

Полный дифференциал функции $z=f(x, y)$ , находится по формуле

$dz = \frac{\partial z}{\partial x} dx + \frac{\partial z}{\partial y} dy$

Частные производные второго порядка находят дифференцированием производных первого порядка:

$\frac{\partial ^{2} z}{\partial x^{2}} = \frac{\partial}{\partial x} \left( \frac{\partial z}{\partial x} \right) \text{ }\text{ } ; \text{ }\text{ } \frac{\partial ^{2} z}{\partial x \partial y} = \frac{\partial}{\partial y} \left( \frac{\partial z}{\partial x} \right) \text{ }\text{ } ; \text{ }\text{ } \frac{\partial ^{2} z}{\partial y \partial x} = \frac{\partial}{\partial x} \left( \frac{\partial z}{\partial y} \right) \text{ }\text{ } ; \text{ }\text{ } \frac{\partial ^{2} z}{\partial y^{2}} = \frac{\partial}{\partial y} \left( \frac{\partial z}{\partial y} \right)$

При нахождении частных производных, правила и таблица производных элементарных функций справедливы и применимы для любой переменной, по которой ведется дифференцирование.

Примеры

ПРИМЕР 1

Задание

Найти частные производные первого порядка функции $z(x, y) = x^{2}-y^{2}+2xy+5$

Решение

Найдем частную производную $\frac{\partial z}{\partial x}$ , при этом $y$ считаем константой. Получим:

$\frac{\partial z}{\partial x} = 2x+2y$

Аналогично находим производную $\frac{\partial z}{\partial y}$ , только теперь дифференцируем по $y$ , а $x$ считаем константой:

$\frac{\partial z}{\partial y} =-2y+2x$

Ответ

ПРИМЕР 2

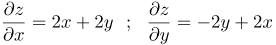Задание

Найти частные производные первого порядка $z=x^{y}$

Решение

Найдем частную производную $\frac{\partial z}{\partial x}$ , при этом $y$ считается константой, и производная берется как от степенной функции:

$\frac{\partial z}{\partial x} =y \cdot x^{y-1}$

Далее найдем частную производную $\frac{\partial z}{\partial y}$ , при этом $x$ считается константой, и производная берется как от показательной функции:

$\frac{\partial z}{\partial y} =x^{y} \ln x$

Ответ

ПРИМЕР 3

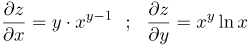Задание

Найти полный дифференциал функции $z=e^{xy}$

Решение

Полный дифференциал функции находится по формуле

$dz = \frac{\partial z}{\partial x} dx + \frac{\partial z}{\partial y} dy$

Найдем частные производные первого порядка. Сначала $\frac{\partial z}{\partial x}$ , при этом дифференцируем по $x$ ; $y$ – константа, а $z=e^{xy}$ будет представлять собой сложную функцию. По правилу дифференцирования сложной функции, имеем

$\frac{\partial z}{\partial x} = e^{xy} \cdot (xy)' = y e^{xy}$

Аналогично находится частная производная $\frac{\partial z}{\partial y}$ , дифференцируется по $y$ , а $x$ считается константой

$\frac{\partial z}{\partial y} = x e^{xy}$

Далее подставляем эти частные производные в формулу для нахождения полного дифференциала, получим

$dz = y e^{xy} dx + x e^{xy} dy \text{ } \Rightarrow \text{ } dz = e^{xy} (y dx + x dy)$

Ответ

$dz = e^{xy} (y dx + x dy)$

ПРИМЕР 4

Задание

Найти все производные второго порядка для функции $z=y^{5}-4x^{2}y^{4}-6x y^{3} +2x-y+3$

Решение

Сначала отыщем все производные первого порядка. При нахождения производной $\frac{\partial z}{\partial x}$ , дифференцируем исходную функцию по $x$ ; $y$ считается константой. Учитывая свойство линейности производной и формулу для вычисления степенной функции, получим

$\frac{\partial z}{\partial x} = -4 \cdot 2xy^{4} -6y^{3} +2\text{ } \Rightarrow \text{ } \frac{\partial z}{\partial x} = -8 xy^{4} -6y^{3}+2$

При нахождения производной $\frac{\partial z}{\partial y}$ , дифференцируем $z$ по $y$ , а $x$ считаем константой, получим:

$\frac{\partial z}{\partial y} = 5y^{4} - 4 \cdot 4x^{2}y^{3} - 6 \cdot 3 xy^{2}-1 \text{ } \Rightarrow \text{ } \frac{\partial z}{\partial y} = 5y^{4} -16x^{2}y^{3}-18 xy^{2}-1$

Теперь перейдем к вычислению производных второго порядка. По определению, вторая производная по $x$ равна $\frac{\partial ^{2} z}{\partial x^{2}} = \frac{\partial}{\partial x} \left( \frac{\partial z}{\partial x} \right)$ . Следовательно, от первой производной $\frac{\partial z}{\partial x}$ нужно взять производную по $x$ , при этом $y$ считаем константой:

$\frac{\partial ^{2} z}{\partial x^{2}} = \frac{\partial}{\partial x} \left( -8 xy^{4} -6y^{3}+2 \right) = -8y^{4}$

Аналогично вычислим частную производную второго порядка по $y$ :

$\frac{\partial ^{2} z}{\partial y^{2}} = \frac{\partial}{\partial y} \left( \frac{\partial z}{\partial y} \right) = \frac{\partial}{\partial y} \left( 5y^{4} -16x^{2}y^{3}-18 xy^{2}-1 \right) = 20y^{3}-54x^{2}y^{2}-36xy$

Вычислим смешанные производные второго порядка. По определению, смешанная производная $\frac{\partial ^{2} z}{\partial x \partial y}$ равна $\frac{\partial}{\partial y} \left( \frac{\partial z}{\partial x} \right)$ , то есть от первой производной $\frac{\partial z}{\partial x}$ нужно взять производную по $y$ , при этом $x$ считаем константой:

$\frac{\partial ^{2} z}{\partial x \partial y} = \frac{\partial}{\partial y} \left( \frac{\partial z}{\partial x} \right) = \frac{\partial}{\partial y} \left( -8 xy^{4} -6y^{3}+2 \right) = -32xy^{3}-18y^{2}$

Производная $\frac{\partial ^{2} z}{\partial y \partial x} = \frac{\partial}{\partial x} \left( \frac{\partial z}{\partial y} \right)$ , то есть от первой производной $\frac{\partial z}{\partial y}$ берем производную по $x$ , а переменную $y$ считаем константой:

$\frac{\partial ^{2} z}{\partial y \partial x} = \frac{\partial}{\partial x} \left( \frac{\partial z}{\partial y} \right) = \frac{\partial}{\partial x} \left( 5y^{4} -16x^{2}y^{3}-18 xy^{2}-1 \right) = -32xy^{3}-18y^{2}$

Ответ

ПРИМЕР 5

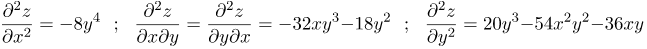Задание

Показать, что функция $z=\sin (2x-3y)$ удовлетворяет уравнению

$\frac{\partial ^{2} z}{\partial x \partial y} = \frac{\partial ^{2} z}{\partial y \partial x}$

Решение

Найдем сначала частные производные первого порядка. По правилу вычисления частных производных, учитывая, что дифференцируемая функция является сложной, получим:

$\frac{\partial z}{\partial x} = \cos (2x-3y) \cdot (2x-3y)_{x}'=2 \cos (2x-3y)$

$\frac{\partial z}{\partial x} = \cos (2x-3y) \cdot (2x-3y)_{y}'= -3 \cos (2x-3y)$

Далее находим смешанные производные второго порядка

$\frac{\partial ^{2} z}{\partial y \partial x} = \frac{\partial}{\partial x} \left( \frac{\partial z}{\partial y} \right) = -3 \sin (2x-3y) \cdot (2x-3y)_{x}' = -3 \cdot 2 \sin (2x-3y) = -6 \sin (2x-3y)$

$\frac{\partial ^{2} z}{\partial x \partial y} = \frac{\partial}{\partial y} \left( \frac{\partial z}{\partial x} \right) = 2 \sin (2x-3y) \cdot (2x-3y)_{y}' = -3 \cdot 2 \sin (2x-3y) = -6 \sin (2x-3y)$

Подставляя в равенство $\frac{\partial ^{2} z}{\partial x \partial y} = \frac{\partial ^{2} z}{\partial y \partial x}$ найденные значения смешанных производных второго порядка, получаем тождество:

$-6 \sin (2x-3y) = -6 \sin (2x-3y)$

Ответ

Функция $z=\sin (2x-3y)$ удовлетворяет уравнению, ее смешанные производные равны.

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Примеры решения частных производных

Теория по частным производным

Примеры