Производная степенной функции

ОПРЕДЕЛЕНИЕ

Производная от степенной функции $x^{n}$ равна произведению показателя степени $n$ на икс в степени на единицу меньше.

$\left( x^{n} \right)' = n x^{n-1}$

Приведенная формула справедлива для любого показателя степени $n$ , будь то натуральное число $1, 2, 3 \ldots$ ; отрицательное число $-1, -2, -3 \ldots$ или дробное число, к примеру $\frac{1}{2}, - \frac{4}{5}$ и т.п.

Примеры решения задач

ПРИМЕР 1

Задание

Найти производную функции

$y(x) = x^{6} - \frac{3}{x^{2}} + \sqrt[3]{x^{4}}-2$

Решение

Искомая производная

$y'(x) = \left( x^{6} - \frac{3}{x^{2}} + \sqrt[3]{x^{4}}-2 \right)'$

Производная от суммы или разности функция равна сумме или разности их производных, то есть

$y'(x) = \left( x^{6} \right)' - \left( \frac{3}{x^{2}} \right)' + \left( \sqrt[3]{x^{4}} \right)' - \left( 2 \right)'$

Производную от $x^{6}$ найдем как производную от степенной функции:

$\left( x^{6} \right)' = 6 \cdot x^{6-1} = 6x^{5}$

Для нахождения производной одночлена $\frac{3}{x^{2}}$ вначале константу вынесем за знак производной:

$\left( \frac{3}{x^{2}} \right)' = 3 \cdot \left( \frac{1}{x^{2}} \right)'$

Далее дробь $\frac{1}{x^{2}}$ представим как степень с отрицательным показателем по свойству $\frac{1}{x^{n}} = x^{-n}$ :

$\left( \frac{3}{x^{2}} \right)' = 3 \cdot \left( \frac{1}{x^{2}} \right)' = 3 \cdot \left( x^{-2} \right)'$

Далее производную находим как от степенной функции:

$\left( \frac{3}{x^{2}} \right)' = 3 \cdot \left( x^{-2} \right)' = 3 \cdot (-2) \cdot x^{-2-1} = -6x^{-3} = -6 \cdot \frac{1}{x^{3}} = -\frac{6}{x^{3}}$

Для нахождения производной $\left( \sqrt[3]{x^{4}} \right)'$ запишем корень в виде степени с дробным показателем:

$\left( \sqrt[3]{x^{4}} \right)' = \left( x^{\frac{4}{3}} \right)'$

Далее производную находим как от степенной функции:

$\left( \sqrt[3]{x^{4}} \right)' = \left( x^{\frac{4}{3}} \right)' = \frac{4}{3} \cdot x^{\frac{4}{3} - 1} = \frac{4}{3} x^{\frac{1}{3}}$

Записываем дробную степень в виде корня:

$\left( \sqrt[3]{x^{4}} \right)' = \frac{4}{3} \sqrt[3]{x}$

Производная от двойки, как от константы, равна нулю:

$\left( 2 \right)' = 0$

Итак, окончательно имеем:

$y'(x) = 6x^{5} - \left( - \frac{6}{x^{3}} \right) + \frac{4}{3} \sqrt[3]{x} - 0 = 6x^{5} + \frac{6}{x^{3}} + \frac{4 \sqrt[3]{x}}{3}$

Ответ

ПРИМЕР 2

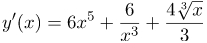Задание

Найти производную функции $y(x)=\left( 2x+7 \right)^{3}$

Решение

Искомая производная

$y'(x) = \left( \left( 2x+7 \right)^{3} \right)'$

Данную производную находим как производную от степенной функции, но так как основание степени $2x+7$ является сложной функцией (отличается от просто $x$ ), то нужно еще умножить на производную от основания:

$y'(x) = \left( \left( 2x+7 \right)^{3} \right)' = 3 \cdot \left( 2x+7 \right)^{3-1} \cdot \left( 2x+7 \right)' = 3 \cdot \left( 2x+7 \right)^{2} \cdot \left( 2x+7 \right)'$

Найдем отдельно оставшуюся производную. Производная о суммы равна сумме производных:

$\left( 2x+7 \right)' = \left( 2x \right)' + \left( 7 \right)'$

Из первого слагаемого вынесем константу за знак производной, а производная от второго, как от константы, равна нулю:

$\left( 2x+7 \right)' = \left( 2x \right)' + \left( 7 \right)' = 2 \cdot \left( x \right)' + 0 = 2 \cdot \left( x \right)'$

Производная от $x$ равна единице:

$\left( 2x+7 \right)' = 2 \cdot \left( x \right)' = 2 \cdot 1 = 2$

Таким образом, производная заданной функции

$y'(x) = 3 \left( 2x+7 \right)^{2} \cdot \left( 2x+7 \right)' = 3 \left( 2x+7 \right)^{2} \cdot 2 = 6 \left( 2x+7 \right)^{2}$

Ответ

$y'(x) = 6 \left( 2x+7 \right)^{2}$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Производная степенной функции

Примеры решения задач