Производная натурального логарифма
![Rendered by QuickLaTeX.com \[ \left( \ln x \right)' = \frac{1}{x} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-7954ad39441756a39575a86b3b00f200_l3.png)
Данную формулу легко получить из формулы производной логарифма по произвольному основанию ![]() , с учетом того, что
, с учетом того, что ![]() и свойств логарифма:
и свойств логарифма: ![]()
![]()
Примеры решения задач
| Задание | Найти производную функции |
| Решение | Искомая производная равна:
Производная логарифма равна единице деленной на подлогарифмическую функцию. И так как последняя является сложной функцией, то еще умножаем на ее производную: Производная синуса равна косинусу: Тогда имеем: |
| Ответ |
| Задание | Найти производную функции |
| Решение | Искомая производная равна:
Вначале берем производную как от степенной функции по формуле Было учтено, что |
| Ответ | 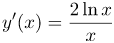 |











