Признаки подобия трапеций

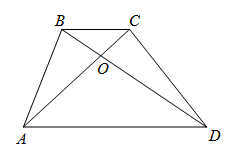
При изучении трапеции выделяют одно из ее свойств: «Диагонали трапеции разбивают ее на четыре треугольника, причем треугольники, прилежащие к основаниям, подобны». Это следует из того, что в треугольниках $BOC$ и $AOD$ (рис. 1) углы при вершине $O$ равны как вертикальные, а $\angle OCB=\angle OAD$ и $\angle OBC=\angle ODA$ как внутренние накрест лежащие.

Примеры решения задач

ПРИМЕР 1

Задание

В трапеции $ABCD\ (BC||AD)\ AD=20$ см $,\ BC=15$ см $,\ O$ – точка пересечения диагоналей, $AO=16$ см. Найти $OC$ .

Решение

Диагонали 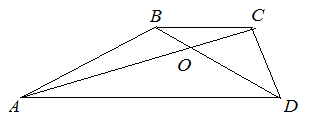$AC$ и $BD$ трапеции $ABCD$ разбивают ее на четыре треугольника. Из свойств трапеции следует, что образовавшиеся треугольники $BOC$ и $AOD$ подобны, а значит,

$\frac{AD}{BC} =\frac{AO}{OC}$

или

$\frac{20}{15} =\frac{16}{OC} \Rightarrow OC=12\ cm$

Ответ

$OC=12$ см

ПРИМЕР 2

Задание	Диагонали трапеции 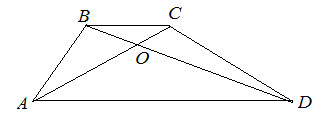$ABCD$ с основаниями $BC$ и $AD$ пересекаются в точке $O,\ BO:OD=3:7,\ BC=18$ см. Найти $AD$ .
Решение	В трапеции $ABCD$ диагонали пересекаются в точке $O$ . Рассмотрим треугольники $BOC$ и $AOD$ . Из свойств трапеции следует, что они подобны. Из условия известно, что $BO:OD=3:7$ , т.е. коэффициент подобия треугольников $k=\frac{3}{7}$ . Тогда $BC=\frac{3}{7} AD\Rightarrow AD=42\ cm$
Ответ	$AD=42$ см

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Признаки подобия трапеций

Примеры решения задач