Свойства подобных треугольников

Определение и свойства подобных треугольников

ОПРЕДЕЛЕНИЕ

Треугольники называются подобными, если их углы равны, а соответствующие стороны пропорциональны.

Подобные треугольники обладают следующими свойствами:

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Отношение периметров и длин либо биссектрис, либо медиан, либо высот, либо серединных перпендикуляров равно коэффициенту подобия, т.е. в подобных треугольниках соответствующие линии пропорциональны.

Примеры решения задач

ПРИМЕР 1

Задание

Треугольники $ABC$ и $A_1 B_1 C_1$ подобны. В треугольнике $ABC$ со стороной $BC=5$ см провели медиану $AM=4$ см. Чему равна медиана $A_1 M_1$ треугольника $A_1 B_1 C_1$ , если $B_1 M_1 =7,5$ см?

Решение

Поскольку треугольники 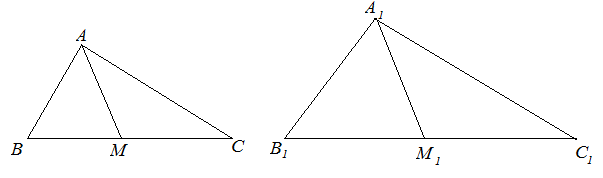$ABC$ и $A_1 B_1 C_1$ подобны, то отношение длин их медиан равно коэффициенту подобия.

Рассмотрим треугольник $A_1 B_1 C_1$ . Так как $A_1 M_1$ – медиана, то

$B_1 C_1 =2B_1 M_1 =15$ см

Найдем коэффициент подобия треугольников:

$k=\frac{BC}{B_1 C_1 } =\frac{5}{15} =\frac{1}{3}$

Тогда

$\frac{AM}{A_1 M_1 } =\frac{4}{A_1 M_1 } =\frac{1}{3} \Rightarrow A_1 M_1 =12\ cm$

Ответ

$A_1 M_1 =12$ см

ПРИМЕР 2

Задание

Треугольники $ABC$ и $A_1 B_1 C_1$ подобны с коэффициентом подобия $k=2$ . Найти периметры этих треугольников, если $AB=3$ см $,\ A_1 C_1 =6$ см $,\ B_1 C_1 =8$ см.