Признаки подобия прямоугольных треугольников
Признак 1. (По острому углу). Если прямоугольные треугольники имеют по равному острому углу, то такие треугольники подобны.
Замечание. У прямоугольного треугольника один угол прямой, поэтому для подобия двух прямоугольных треугольников достаточно, чтобы у них было по равному острому углу.
Признак 2. (По двум катетам). Если катеты одного прямоугольного треугольника пропорциональны катетам второго прямоугольного треугольника, то такие треугольники подобны.
Признак 3. (По катету и гипотенузе). Если катет и гипотенуза одного прямоугольного треугольника пропорциональны катету и гипотенузе второго прямоугольного треугольника, то такие треугольники подобны.
Примеры решения задач
| Задание | В треугольнике |
| Решение | Сделаем рисунок.
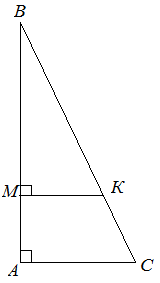
Тогда искомая сторона |
| Ответ |
|
| Задание | В прямоугольном треугольнике |
| Решение | Сделаем рисунок.
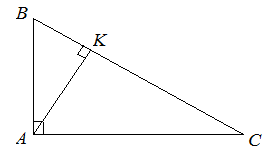
или откуда
|
| Ответ |
|











