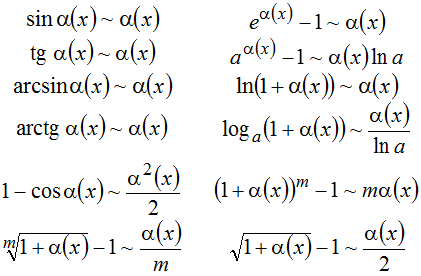Сравнение бесконечно малых функций

Пусть функции $\alpha \left( x \right)$ и $\beta \left( x \right)$ являются бесконечно малыми функциями в точке $x=a$ , то есть

$\underset{x\to a}{\mathop{\lim }}\,\alpha \left( x \right)=0,\ \underset{x\to a}{\mathop{\lim }}\,\beta \left( x \right)=0$

и пусть существует предел их отношения $\underset{x\to a}{\mathop{\lim }}\,\frac{\alpha \left( x \right)}{\beta \left( x \right)}$ , который равняется $q$ :

$\underset{x\to a}{\mathop{\lim }}\,\frac{\alpha \left( x \right)}{\beta \left( x \right)}=q$

Тогда если:

1) $q$ – это конечное, отличное от нуля число, то бесконечно малые функции $\alpha \left( x \right)$ и $\beta \left( x \right)$ называются бесконечно малыми функциями одного и того же порядка;

2) $q=0$ , то функция $\alpha \left( x \right)$ называется бесконечно малой функцией более высокого порядка, чем функция $\beta \left( x \right)$ ;

3) $q=\infty$ , то функция $\beta \left( x \right)$ называется бесконечно малой функцией более высокого порядка, нежели $\alpha \left( x \right)$ .

4) $q=1$ , то функции $\alpha \left( x \right)$ и $\beta \left( x \right)$ называются эквивалентными бесконечно малыми функциям.

ПРИМЕР

Задание

Сравнить порядок бесконечно малых функций $\alpha \left( x \right)=\sin x$ и $\beta \left( x \right)={{x}^{2}}$ в точке $x=0$

Решение

Для сравнения найдем предел отношения заданных функций при $x\to 0$ :

$\underset{x\to 0}{\mathop{\lim }}\,\frac{\sin x}{x}$

Полученный предел является первым замечательным пределом и его значение равно 1:

$\underset{x\to 0}{\mathop{\lim }}\,\frac{\sin x}{x}=1$

А тогда делаем вывод, что заданные функции являются эквивалентными бесконечно малыми функциями (поскольку $q=1$ ).

Ответ

Эквивалентные бесконечно малые функции.

Эквивалентные бесконечно малые функции играют особую роль среди всех бесконечно малых функций.

Теоремы для сравнения бесконечно малых функций

ТЕОРЕМА

Предел отношения двух бесконечно малых функций не изменится, если каждую или одну из них заменить эквивалентной ей бесконечно малой:

$\begin{matrix} \alpha \left( x \right)\sim {\ }{\alpha }'\left( x \right) \\ \beta \left( x \right)\sim {\ }{\beta }'\left( x \right) \\ \end{matrix}x\to a\Rightarrow \underset{x\to a}{\mathop{\lim }}\,\frac{\alpha \left( x \right)}{\beta \left( x \right)}=\underset{x\to a}{\mathop{\lim }}\,\frac{{\alpha }'\left( x \right)}{{\beta }'\left( x \right)}=\underset{x\to a}{\mathop{\lim }}\,\frac{{\alpha }'\left( x \right)}{\beta \left( x \right)}=\underset{x\to a}{\mathop{\lim }}\,\frac{\alpha \left( x \right)}{{\beta }'\left( x \right)}$

ТЕОРЕМА

Разность двух эквивалентных бесконечно малых функций есть бесконечно малая более высокого порядка, чем каждая из них.

ТЕОРЕМА

Если разность бесконечно малых функций $\alpha \left( x \right)$ и $\beta \left( x \right)$ есть бесконечно малая высшего порядка, чем эти функции, то функции $\alpha \left( x \right)$ и $\beta \left( x \right)$ являются эквивалентными бесконечно малыми.

ТЕОРЕМА

Сумма конечного числа бесконечно малых функций разных порядков эквивалентна слагаемому низшего порядка.

Слагаемое, которое эквивалентно сумме бесконечно малых, называется главной частью этой суммы.

Замена суммы бесконечно малых функций ее главной частью называется отбрасыванием бесконечно малых высшего порядка.

ПРИМЕР

Задание

Найти предел

$\underset{x\to 0}{\mathop{\lim }}\,\frac{3{{x}^{2}}+7{{x}^{3}}}{3x+5{{x}^{2}}-6{{x}^{3}}}$

Решение

Данный предел содержит неопределенность типа

$\left[ \frac{3\cdot {{0}^{2}}+7\cdot {{0}^{3}}}{3\cdot 0+5\cdot {{0}^{2}}-6\cdot {{0}^{3}}}=\frac{0}{0} \right]$

Отбросим в числителе и знаменателе дроби, стоящей под знаком предела, бесконечно малые более высоких порядков (то есть заменим каждую суму ее главной частью), получим:

$\underset{x\to 0}{\mathop{\lim }}\,\frac{3{{x}^{2}}+7{{x}^{3}}}{3x+5{{x}^{2}}-6{{x}^{3}}}\ \left[ \frac{0}{0} \right]=\underset{x\to 0}{\mathop{\lim }}\,\frac{3{{x}^{2}}}{3x}=\underset{x\to 0}{\mathop{\lim }}\,x=0$

Ответ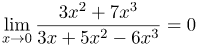

Приведем таблицу эквивалентных бесконечно малых функций в точке $x=a$ ( $\underset{x\to a}{\mathop{\lim }}\,\alpha \left( x \right)=0$ ):

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Сравнение бесконечно малых функций

Теоремы для сравнения бесконечно малых функций