Замечательные пределы
Первый замечательный предел:
![]()
Следствия:
![]()
![]()
![]()
![]()
Подробнее про первый замечательный предел читайте в отдельной теме.
Примеры решений с первым замечательным пределом
| Задание | Найти предел
|
| Решение | Вначале выясним тип неопределенности (если она есть). Для этого подставим предельное значение 0 в выражение под знак предела:
Таким образом, у нас есть неопределенность вида По свойствам пределов константу можно выносить за знак предела, а тогда |
| Ответ | 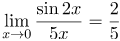 |
Второй замечательный предел
![Rendered by QuickLaTeX.com \[ \underset{x\to \infty }{\mathop{\lim }}\,{{\left( 1+\frac{1}{x} \right)}^{x}}=e \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-1736bc90e2d453cd49d261e62217ba41_l3.png)
здесь ![]() – постоянная Эйлера
– постоянная Эйлера
Следствия:
![]()
![]()
![]()
![]()
![]()
Подробнее про второй замечательный предел читайте в отдельной теме.
Примеры решений со вторым замечательным пределом
| Задание | Найти предел
|
| Решение | Выясним тип неопределенности (если он есть). Основание степени имеет предел
а степень Таким образом, имеем неопределенность типа Приведем заданный предел ко второму замечательному: |
| Ответ | 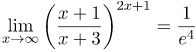 |






![Rendered by QuickLaTeX.com \[\underset{x\to \infty }{\mathop{\lim }}\,\frac{x+1}{x+3}\ \left[ \frac{\infty }{\infty } \right]=\underset{x\to \infty }{\mathop{\lim }}\,\frac{x\left( 1+\frac{1}{x} \right)}{x\left( 1+\frac{3}{x} \right)}=\underset{x\to \infty }{\mathop{\lim }}\,\frac{1+\frac{1}{x}}{1+\frac{3}{x}}=\frac{1+0}{1+0}=1\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-56efe0b9277918f0d1903bc88ee4173d_l3.png)
![Rendered by QuickLaTeX.com \[=\underset{x\to \infty }{\mathop{\lim }}\,{{\left( 1+\frac{-2}{x+3} \right)}^{2x+1}}=\underset{x\to \infty }{\mathop{\lim }}\,{{\left[ \underbrace{{{\left( 1+\frac{-2}{x+3} \right)}^{\frac{x+3}{-2}}}}_{\to e} \right]}^{\frac{-2}{x+3}\cdot \left( 2x+1 \right)}}=\underset{x\to \infty }{\mathop{\lim }}\,{{e}^{\frac{-4x-2}{x+3}}}=\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-f3e61dbd3fa4ca0341853a366490d7c1_l3.png)
![Rendered by QuickLaTeX.com \[={{e}^{\underset{x\to \infty }{\mathop{\lim }}\,\frac{-4x-2}{x+3}\left[ \frac{\infty }{\infty } \right]}}={{e}^{\underset{x\to \infty }{\mathop{\lim }}\,\frac{x\left( -4-\frac{2}{x} \right)}{x\left( 1+\frac{3}{x} \right)}}}={{e}^{\underset{x\to \infty }{\mathop{\lim }}\,\frac{-4-\frac{2}{x}}{1+\frac{3}{x}}}}={{e}^{\frac{-4-0}{1+0}}}={{e}^{-4}}=\frac{1}{{{e}^{4}}}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-dd3c3f10cde338b88da5f699c412b7a0_l3.png)





