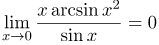Таблица эквивалентности пределов
Пусть функция ![]() является бесконечно малой функцией в точке
является бесконечно малой функцией в точке ![]() , то есть
, то есть
![]()
тогда имеют место следующие соотношения:
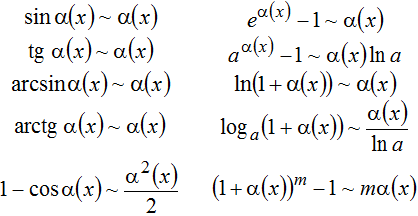
Примеры решения задач
| Задание | Найти предел
|
| Решение | Выясним, имеет ли рассматриваемый предел неопределенность и если да, то какого типа:
То есть имеем неопределенность типа К знаменателю дроби применим формулу сокращенного умножения «разность квадратов»: |
| Ответ | 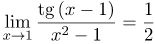 |