Первый замечательный предел
Формула первого замечательного предела
![]()
![]()
Доказательство первого замечательного предела
Рассмотрим односторонние пределы
![]()
Докажем, что каждый из этих пределов равен единице. Тогда и предел ![]() также будет равняться единице.
также будет равняться единице.
Пусть ![]() и отложим этот угол на тригонометрической окружности (рис. 1).
и отложим этот угол на тригонометрической окружности (рис. 1).
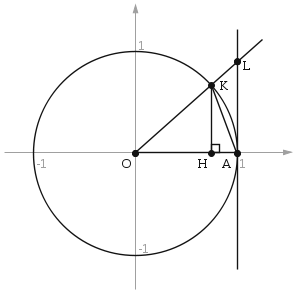
Рис. 1
Этот луч будет пересекать единичную окружность в точке ![]() , а вертикальную касательную, проведенную в точке
, а вертикальную касательную, проведенную в точке ![]() , – в точке
, – в точке ![]() . Через точку
. Через точку ![]() обозначим проекцию точки
обозначим проекцию точки ![]() на горизонтальную ось косинусов.
на горизонтальную ось косинусов.
Рассмотрим треугольники ![]() и круговой сектор
и круговой сектор ![]() . Очевидно следующее двойное неравенство:
. Очевидно следующее двойное неравенство:
![]()
Абсцисса точки ![]() равна
равна ![]() , а ее ордината –
, а ее ордината – ![]() (равна высоте
(равна высоте ![]() ). А тогда
). А тогда
![]()
Здесь ![]() как радиус тригонометрической окружности.
как радиус тригонометрической окружности.
Площадь центрального сектора круга радиуса ![]() с центральным углом
с центральным углом ![]() равна
равна
![]()
Площадь ![]()
![]()
Итак, неравенство (1)перепишется в виде:
![]()
Так как для ![]() все части этого неравенства положительны, поэтому его можно записать следующим образом:
все части этого неравенства положительны, поэтому его можно записать следующим образом:
![]()
После умножения на ![]() получаем:
получаем:
![]()
или
![]()
Переходя во всех частях последнего неравенства к пределу при ![]() , будем иметь:
, будем иметь:
![]()
![]()
По теореме о двухстороннем ограничении (теорема «про двух милиционеров») делаем вывод, что и
![]()
Вычислим теперь ![]() :
:
![]()
![]()
То есть ![]() .
.
А, таким образом, и ![]() .
.
Теорема доказана.
Следствия из первого замечательного предела
![]()
![]()
![]()
![]()
Примеры решения задач
| Задание | Вычислить предел
|
| Решение | Вначале выясним тип неопределенности, для этого в выражение, стоящее под знаком предела подставим значение Таким образом, имеем неопределенность типа Предел частного равен частному пределов, если последние существуют: Предел константы равен этой константе: а предел знаменателя есть первый замечательный предел и |
| Ответ | 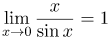 |
| Задание | Вычислить предел
|
| Решение | Выясним тип неопределенности (если она есть). Для этого вместо Итак, имеем неопределенность типа Получили первый замечательный предел, тогда: |
| Ответ | 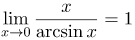 |






![Rendered by QuickLaTeX.com \[\underset{x\to 0}{\mathop{\lim }}\,\frac{x}{\sin x}\ \left[ \frac{0}{0} \right]=\underset{x\to 0}{\mathop{\lim }}\,\frac{1}{\frac{\sin x}{x}}\overset{?}{\mathop{=}}\,\frac{\underset{x\to 0}{\mathop{\lim }}\,1}{\underset{x\to 0}{\mathop{\lim }}\,\frac{\sin x}{x}}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-9ed1cdb3067c4684b8339765e5cad7ed_l3.png)
![Rendered by QuickLaTeX.com \[\underset{x\to 0}{\mathop{\lim }}\,\frac{x}{\arcsin x}\ \left[ \frac{0}{0} \right]\ \left\| \begin{matrix} & \arcsin x=y \\ & x=\sin y \\ & y\to 0 \\ \end{matrix} \right\|=\underset{x\to 0}{\mathop{\lim }}\,\frac{\sin y}{y}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-fb24ec179a173385e5c4035f4f07f893_l3.png)
![Rendered by QuickLaTeX.com \[\underset{x\to 0}{\mathop{\lim }}\,\frac{x}{\arcsin x}\ \left[ \frac{0}{0} \right]\ \left\| \begin{matrix} & \arcsin x=y \\ & x=\sin y \\ & y\to 0 \\ \end{matrix} \right\|=\underset{x\to 0}{\mathop{\lim }}\,\frac{\sin y}{y}=1\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-65796f2c53515e101fdc90efba07b405_l3.png)





